Тетрадь 6
/Авторский коллаж на основе рисунков из Интернет источников в свободном доступе. В центре – картина Р.Делоне «Бесконечные ритмы»/
…Мысль летуча.
…Звук летуч.
Ключи знают тайну, но хранят молчание.
Мысль облачается в звук. Ключи открывают вход-выход. Мысль звучит и …исчезает. Неуловима. Кто узнает о ней, когда смолкнут звуки?
ЗаПЕЧАТлеть! – Отражение, тень, оттиск – портрет на память. Печать мгновения.
Кто з н а е т тайну печатей, тот открывает их, — и развёртываются свитки Мысли, вновь облачаясь в звуки.
Пожалуй, тебе известно, что NOTA имеет смысл «знак».
Откуда слово nota? – Предполагают, что из старинного слова gnata, которое связано глубоким родством со словом gnoscere – «знать».
«Знать» — это, конечно же, не просто получать информацию (иначе превратишься в кладовку, где хранятся случайные неупорядоченные вещицы). Настоящее знание вырастает из п о н и м а н и я и в н и м а н и я.
Внимать в себя, сопоставлять с тем, что уже внял до; сравнивать, упорядочивать, организовывать; находить родство, связи, аналогии. Подобия…
Клавиатура-«ключница» явила нам великий фундаментальный Закон квинт.
Как он заПЕЧАТлел себя в нотной записи – думаю, ты догадываешься, ибо он и здесь проявил свою фундаментальность:
Стан! – На нём весь храм музыки держится, как на фундаменте. Стан – стал.
На нём всё время происходит с т а н о в л е н и е гармоний-аккордов, мелодий. Вся их изменчивость – на фундаменте порядка.
Как он протяжён! Бесконечен, как музыка всех времён.
Чем он ещё любопытен? Допускает ли он случайности-вольности, — например, в пространственном расположении своих пятилинейных полос?
Давай проверим? Поэкспериментируем?
/Рис. автора/
Итак, верхняя полоса – для квинт вверх, нижняя – для квинт вниз.
А между…
Пространство для ещё одной – подразумеваемой, невидимой – квинты.
Размыкание.
Для новых возможностей. Для перекрёстов правого и левого, верхних и нижних звуков – на добавочных линиях. Для связи.
В геометрии – для подобий.
Подобное размыкание мы видели и в Сфере Александера, и в пентаграммах, и в Снежинке Коха…
Принцип Фракталов: Целое делится на 3 части, вычитается 1/3 (остаются 2/3); эта 1/3 становится новым Целым, новое Целое делится на 3 части, вычитается 1/3 (остаются 2/3); эта вновь полученная 1/3 становится следующим новым Целым, делится на 3… И всё повторяется подобно. И бесконечно.
Эта же операция использована и в Принципе Флейт – для получения
т е м п е р и р о в а н н о г о с т р о я.
Логика (logos) этого строя отПЕЧАТался и в нотной записи – как в записи
з н а н и я о «фундаменте» мира, его о с н о в е.
А мы?
ОтПЕЧАТываемся мы сами в музыкальном строе и его отПЕЧАТке?
/Рис. из Интернет источников в свободном доступе. Пометки автора/
Этим рисункам около 30 000 лет. Они – из пещеры Альтамира в Испании.
И в самом деле, наши руки – квинты влево, квинты вправо, а между, в «размыкании» рук, — узел, связь: перекрёсты мозговых полушарий, перекрёсты сосудов в сердце; наша жизнь – биологическая и душевная, её пульсация и волны дыхания, её импульсы… Вертикаль нашего тела и нашего духа, аккорд.
Мы – напротив первой октавы, соответствующей нашему умеренно-спокойному голосу. Она для нас – «диапазон отсчёта». Точка отсчёта в нашей системе координат – ДО (нота). От неё – горизонталь клавиатуры влево и вправо и вертикаль звуков вверх и вниз.
Итак, мы выбрали систему координат в мире звуков, которая соответствует нашему голосу – среднему такому человеческому голосу. А в этой системе координат выбрали нулевую точку отсчёта – ДО (нота, звук и его ключ/клавиша на клавиатуре).
От этой нулевой точки отсчёта мы можем двигаться по клавиатуре вправо, и её ключи-клавиши будут открывать ход звукам вверх (высокие звуки).
От этой же нулевой точки мы можем двигаться по клавиатуре влево, и её ключи-клавиши будут открывать ход звукам вниз (низкие звуки).
Все ключи-клавиши и звуки, которым они открывают ход, будут подчиняться двум главным ключам. Один из них – ключ «ВЕРХ» (точнее – «ВЕРХ-ПРАВО»), другой – ключ «НИЗ» («НИЗ-ЛЕВО»).
Ключ «ВЕРХ» получил собственное имя – ключ «СОЛЬ» (шаг на квинту вверх от нулевой точки ДО). «Скрипичным» этот ключ, очевидно, стали называть по трём главным причинам:
- Скрипка звучит высоко. Гулкие басы – не для неё.
- Скрипка – инструмент струнный. А ведь именно струны когда-то продемонстрировали нам особенности поведения звуковой волны: любая звуковая волна модулирует (изменяется) только в сторону более высоких тонов (обертонов). Попросту говоря, любая звуковая волна может изменяться только «вверх». И это было показано Пифагором на струнах.
- Скрипка подражает непрерывности звуковой волны. Она подражает непрерывности голоса – переливающимся друг в друга последовательным звукам. Скрипка – сама м е л о д и я. Скрипичный ключ – ключ к связности, непрерывности, мелодии. Вот где пространство его власти.
Ключ «НИЗ» получил собственное имя – ключ «ФА» (шаг на квинту вниз от нулевой точки ДО). Шаги вниз ведут к басам (до инфразвуков). Мы знаем, что ключ «ФА» — «Басовый». В басах – мощь. И эта мощь подчёркивается звуковой массой – аккордами. Аккорды по преимуществу там, где власть басового ключа.
Как всё это умозрение о главных ключах отразилось-отпечаталось в их изображениях?
Ключ «СОЛЬ»
В его имени-названии звучат как минимум два смысла: соло и Солнце.
Соло – от лат. solus – «один».
Солнце для нас – тоже одно. Одна такая особенная звезда, хотя и подобная многим звёздам, но в то же время н е п о в т о р и м а я. Неповторимая хотя бы потому, что именно близ неё возникла Жизнь – та, какую мы знаем и какую не можем обнаружить больше нигде во Вселенной.
Так и мы, люди, подобны друг другу как вид Человек, но каждый из нас – соло: неповторим; со своим неповторимым голосом и неповторимой мелодией.
И в то же время, всё разнообразие музыки (как и неповторимых «музык» наших человечьих жизней) держится и связывается Законом квинт – квинт, движущихся вслед за Солнцем (вместе с нашей планетой Землёй) ввысь, «по Солнцу», «по свету».
Вот как смыслы ключа «СОЛЬ» могут отпечатываться в геометрии его знака:
/Рис. из Интернет источника в свободном доступе/
Здесь мы увидим и вертикаль восхождения; и волну, и спираль, – которые «перетекают» друг в друга, преобразуются друг в друга и, в конце концов, утверждают квинту СОЛЬ в системе координат от нулевой точки ДО.
Здесь, на пересечениях прямых линий, а также прямых с линиями круженья, мы обнаружим и проявление равенства, и проявление неравенства – как при построении Золотого сечения. И принцип Фрактала можно обнаружить здесь.
В общем, геометрия ключа «СОЛЬ» связана с геометрией, которая выражает явление связности, непрерывности.
Мы любопытны?
Ещё как!
Мы любим тайны?
А кто же их не любит!..
У нас есть ключ. Должны быть и тайны! Ключ – к тайнам.
Тайна №1.
Входи и смотри (зрением ума, разумеется).
/Рис. автора/
Вертикаль ключа, поднимаясь снизу вверх (по правилу обертонов, в соответствии с природой звука), охватывает и гептатонику ( она же – и диатоника, и гамма), и охватывает октаву (расстояние-интервал от примы – тоники – до её повторения вверху, то есть до октавного звука).
Это показывает нам система звуковых координат из линеек.
Сама вертикаль поднимается от нашей «нулевой точки отсчёта» – ДО, которую мы называем «первой» (примой), дорастает до октавного повторения примы (по количеству линеек!) и делает возвратную петлю в виде волны и спирали, которая завершается точкой, обозначающей звук (звук!) квинты.
Нижняя граница спирали намекает на то, что квинта может быть заполнена ещё одним звуком – третьим, т е р ц и е й.
И тогда образуется т р е звучие — аккорд.
Т о н и ч е с к о е т р е з в у ч и е — от начального т о н а (звука).
Любопытно, что высота столбика (или колонны?) трезвучия геометрически равна ширине спирали ключа.
А сами ноты – словно маленькие подобия этой спирали. И они – не шарики, а эллипсоиды – как наша планета Земля.
Тонкий расчёт – в основе геометрии нотного стана!
А ты помнишь то трезвучие, что явилось нам в Сфере Александера?
Вот чудо обнаружилось:
Если квинту «ДО – СОЛЬ» просчитать хроматическими звуками, то по количеству звуков она окажется о к т а в о й (до-до#-ре-ре#-ми-фа-фа#-соль – 8 звуков), а терция «ДО – МИ» окажется по количеству хроматических звуков к в и н т о й (до-до#-ре-ре#-ми – 5 звуков). Что за чудесные превращения!
Тайна №2.
Сущая головоломка!
Но – захватывающая. И уж точно – геометрическая.
Давай сделаем (умозрительно) печать звука – печать-ноту, эллипсоид: его вертикальная ось – размером от линейки стана до линейки, горизонтальная ось – чуть больше.
Пропечатаем подряд все звуки в диапазоне, который охватывает ключ «СОЛЬ» на нотном стане:
/Рис. автора/
Что мы увидим?
Мы увидим, что ноты образовали восходящую линию.
Если мы измерим длину этой линии, то окажется, что эта самая длина является длиной окружности, диаметром которой является высота скрипичного ключа! Проверь сам.
(На моём настоящем рисунке высота ключа – 3,5см; длина линии нот ≈ 11см.
3,5 х 3,14 = 10,99. Ты же помнишь, что длина окружности вычисляется по формуле L=πD.)
Вот ещё как может маскироваться круженье.
Мы видим, что ноты образовали диагональ.
Ключ указывает на вертикаль, а линии нотного стана – горизонталь.
Сам собою напрашивается треугольник. Даже два треугольника.
Но мы пока поиграем-поэкспериментируем с одним.
Давай вырежем его из бумаги и накрутим на вертикаль ключа (подойдёт соломинка для коктейля диаметром с ноту на нашем рисунке).
/Рисунки атора/
Мы увидим спираль!
Если соломинка оказалась действительно диаметром с ноту, мы увидим семь витков спирали – как семь нот гаммы (диатоники).
А ведь мы, можно сказать, закручивали диапазон октавы (от линейки до линейки, как показывает вертикаль ключа). Просто волшебство какое-то.
Есть ещё более изумительное волшебство в нашем рисунке с ключом и нотами.
Вертикаль ключа показывает нам октаву, а диагональ звуков – две октавы, укладывающиеся в октаву ключа.
Когда учёные, занимающиеся квантовой физикой (наисовременнийший раздел физики), пришли в результате своих исследований к модели пространства, они обнаружили, что само пространство обладает особой
в р а щ а т е л ь н о й с и м м е т р и е й. В этом пространстве сфера совершает полный поворот не в 360˚, а в 720˚ — то есть, поворот вдвое больший на самом деле.
Получается, что ноты демонстрируют нам аналогичное явление.
Как это явление объясняют сами физики, ты сможешь прочитать в небольшой, но очень доступной для понимания и увлекающей своей живостью статье-эксперименте Сета Ллойда, профессора квантовомеханической инженерии (из книги Джона Брокмана «Теории всего на свете». М.,Лаборатория знаний, 2019г.). Вот цитата из статьи, об итоге эксперимента с вращением мяча в руке:
«…вы обнаружите, что траектория мяча походит на изображённую в пространстве восьмёрку или знак бесконечности (∞) и что траектория эта совершила не один полный поворот, а два. Таким образом, истинная симметрия пространства соответствует повороту не на 360˚, а на 720˚.»
Подобное явление можно обнаружить и в эксперименте на плоскости, с кругами: когда один круг совершает поворот вокруг своей копии (как самого себя же).
Посмотри и поэкспериментируй.
Мы экспериментируем на плоскости, которая служит нам сейчас в качестве проекции пространства (как плоские тени от объёмных предметов).
Синяя точка на рисунке отмечает начальное положение.
Когда круг А сам по себе в результате своего движения будет выглядеть так же, как он выглядит сам по себе на первом рисунке (с той же синей точкой справа), это будет означать, что он совершил поворот на 360˚ вокруг своего центра.
Начальное положение круга А:
Начинаем катить круг А по линии окружности другого круга:
Круг А выглядит так же, как в начале своего пути. Он совершил поворот на 360˚, но в начальное положение не вернулся. Ты можешь проверить это практически, вырезав круги из картона. Ты можешь о с я з а т ь этот геометрический процесс.
Катим круг А дальше:
Круг А повернулся ещё на 360˚ и вернулся в начальное положение.
Итого он совершил поворот на 720˚.В этом явлении удивительно вот что:
Обе начальные окружности (чёрная и круга А) совершенно одинаковы, с одинаковым количеством точек, из которых состоят. При движении круга А все точки его окружности должны были совпасть с точками чёрной окружности «точка в точку», — допустим, на каждый градус поворота – по точке. Но градусов поворота оказалось в два раза больше, — как будто у окружности круга А и точек в два раза больше.
Подобному явлению удивлялся и немецкий математик Георг Кантор, только по поводу графиков функции. Он удивлялся тому, что количество точек отрезка равно количеству точек квадрата. Только в случае с функцией две точки координат сливаются в одну точку функции. Этот пример – из книги В.Босса «Интуиция и математика». Кантор говорил, что его рассудок отказывается это принимать, но очевидность – убедительна.
Вообще, вся эта геометрическая картинка заставила вспомнить знаменитые эпициклы Птолемея. В его космической системе планеты двигались подобным образом. Знал ли Птолемей об истинной вращательной симметрии пространства? Тогда квантовой механики ещё не было… Система Птолемея, в конце концов, была отвергнута последующими поколениями астрономов, но до сих пор даже современных учёных удивляет точность, с которой эта система предсказывала явление планет, их движение на земном небосклоне.
А теперь просто посмотри на продолжение этой геометрической игры:
Если соединить точки вращения круга А…
Лист? Сердце?
А если почаще наносить точки вращения… (Ты можешь проэкспериментировать сам, с помощью кругов.)
Сердце? Яблоко?
А это – знаменитая к а р д и о и д а, математический объект, из книги К.Пиковера «Великая математика».
Согласись, что музыкальная геометрия – геометрия нотного стана – выглядит намного компактнее. И весьма лаконично она даёт нам знать («нота» — «знать») об истинной вращательной симметрии пространства. К тому же – эта геометрия звучит!
Тайна №3.
На самом деле в этой тайне для нас нет ничего тайного. Нужно только суметь
у в и д е т ь некоторые отношения, пропорции в геометрии ключа – и всё!
/Рисунки автора/
Дальше – чуть поинтереснее. Присмотрись.
/Рис. автора/
Конечная точка большого завитка может указывать и на квинту, и на кварту.
А никакого страшного противоречия нет. Мы-то хорошо знаем, что кварта – это всего лишь перевёртыш квинты: как будто её отражение в зеркале, где правое и левое меняются местами.
В конце концов, нота СОЛЬ может быть не только квинтой До-мажора, но и до-минора; может быть квартой Ре-мажора и ре-минора.
Это всего лишь говорит о великих потенциальных возможностях ключа. По опыту ты знаешь, что в с е тональности пользуются его услугами!
Так что… как посмотреть. А «как посмотреть» — это значит выбрать систему отсчёта и как и что в ней соотносить. И это – принцип относительности.
Вот! В музыке тоже действует принцип относительности.
Тайна №4.
Геометрия в пространстве.
Возьмём Геометрию за ручку и выведем прогуляться в пространство.
Мы будем с нею играть. А как же!
Пусть линия станет полоской бумаги ≈ 5мм шириной и 300мм длиной.
Раз-два-три — начало игры! Смотри и повторяй:
/Рис. автора/
Совет: начинай снизу вверх, по логике звука и нотного стана. В любой игре обязательно есть логика.
Получилось?
…Результаты экспериментов принято изучать, анализировать.
И мы попробуем.
Первая петля:
Если мы её склеим в обозначенной точке, у нас получится Петля Мёбиуса ( она же – Лента Мёбиуса). Она будет обладать свойствами Ленты Мёбиуса, даже если мы склеим концы нашей ленты под прямым углом.
Напомню свойства этой Ленты:
- Непрерывность.
- Парадокс: две поверхности ленты на самом деле являются одной поверхностью для скользящего по ленте пальца. Наш палец скользит всё время в одном направлении непрерывно, не перескакивая с одной поверхности на другую, но при этом бывает на обеих поверхностях.
Два – в одном, одно – из двух. Два – как одно.
Этот парадокс удивлял и Георга Кантора в связи с графиком функции (кол-во точек квадрата из координат (а их две) то же, что и в получаемом отрезке из одиночных точек. Этот же парадокс и во вращательной симметрии пространства, и… в геометрии нотного стана.
И вот ещё сам ключ намекает на это же своей петлёй.
Тут надо приплюсовать и третье свойство Ленты (Петли) – бесконечность.
Продолжим?
Сделай так и затяни аккуратно концы ленты.
…Моя лента совершила вращательное движение в пространстве и успокоилась на такой знакомой фигуре! Вот на этой:
/Рисунки автора/
Как тебе такое?
Скрипичный ключ – зашифрованный узел?!
Выходит, что так. К тому же, узел – мы знаем – обладает свойствами Ленты Мёбиуса, когда замкнут.
Сам узел может выполнять функцию склейки в Ленте Мёбиуса. Он ведь переворачивает, меняет местами противоположности: верх-низ, лево-право.
Давай сравним ключ и свободный замкнутый узел:
Три петли (зелёные точки). Три пересечения (красные точки).
Трезвучие.
Со второй фигурой можно играть в обращения трезвучий, если катить её, словно колесо:
/Рисунки автора/
Начинаем снизу и кружимся вверх – по правилу поведения звука (обертонов); слева направо – по правилу устроения клавиатуры.
Ох, что-то это напоминает…
Движение планет и самой солнечной системы тебе это не напоминает?
/Рис. из Интернет источника в свободном доступе/
А давай покатаем колесо (круг то есть). Играть так играть!
Мы это делали, когда вникали в истинную вращательную симметрию пространства. Только у нас теперь будет круг с тремя точками-нотами: ДО-МИ-СОЛЬ, трезвучие.
…У меня вот что получилось:
Три «кардиоиды»!
А ты можешь проверить всё сам, экспериментально. Круги в кармашке слева.
Отметь все три точки в начальном положении и продолжай отмечать, когда начнёшь катить, то есть вращать, «трезвучие». И так – пока наше трезвучие не вернётся в начальное положение.
Круговое вращение вернуло нас к петлям!
Давай поисследуем: что мы здесь интересненького разглядим?
Геометрическая прогрессия (k=2, или ½).
Квинтовые отношения.
/Рисунки автора/
Подобия с намёком на чередование.
Подобное чередование мы видели в проволочном «еже», выращенном из проволок, размеченных в соответствии с числами Фибоначчи.
Напомню:
/Модель автора/
Внутри – красный додекаэдр, он вырастает в белый икосаэдр, а тот опять вырастает в додекаэдр, показанный синим цветом.
Фигура, которая образуется, когда завязываешь узел.
Прозрачный узел в процессе завязывания.
На первый взгляд даже трудно вообразить, что это всё – в скрипичном ключе!..
Но выходит, что в очень разных и непохожих внешне формах и явлениях можно обнаружить общую связь.
Мы всего лишь меняли точки зрения – «системы отсчёта».
Вот ещё одна точка зрения.
Что если бы мы завязали наш скрипичный ключ-узел не из плоской ленты, а из круглой верёвочки?
Чтобы завязать плоский узел, нам хватило бы шести квадратов на ленте.
Это чертёж узла.
/Рисунки автора./
Чтобы завязать узел из круглой верёвочки, нам хватит её длины, равной шести цилиндрическим кусочкам; при этом высота и диаметр каждого цилиндрика равны (тот же квадрат). Можешь проверить практически.
А ещё в объём этого отрезка верёвочки помещается объём девяти сфер (по закону Архимеда объём сферы, вписанной в цилиндр, равен 2/3 объёма цилиндра). 9/6 = 3/2. Квинта! Верёвочный узел тоже покажет квинту.
Но мы вернёмся к плоскости, скрипичному ключу и вращению трезвучия.
Ключ = узел.
Ключ указывает на трезвучие.
Трезвучие вращается-обращается:
1-е обращение – секстаккорд ( «секст» — «шесть», «секста» — «шестая»).
2-е обращение – квартсекстаккорд ( «кварт» — «четыре», «кварта» — «четвёртая»).
Когда мы завязываем узел, вращая ленту, первый поворот нарисует 6 в виде шестиугольника.
После следующего поворота мы продеваем ленту в петлю, и она рисует нам квадраты-кварты.
/Рис. автора/
Затянутая петля превращается в пятиугольник-квинту. А в квинту заключено и трезвучие в своём начальном виде – из двух терций.
Выходит, геометрия скрипичного ключа содержит в себе намёк и на обращения трезвучия: секстаккорд и квартсекстаккорд. Удивительны свойства этого ключа!
А для чего вообще трезвучиям нужно вращаться?
А для того же, для чего вращаются электроны в атомах и все космические тела – для связи, для преобразований; для того, чтобы атомы с помощью электронов соединялись друг с другом; чтобы космические пылинки образовывали звёзды и планеты, а из них – галактики… Переменами и связью держится жизнь.
Тонические трезвучия тональностей на самом деле не прыгают по квинтам, когда ТОНАЛЬНОСТИ-актрисе захочется смодулировать – измениться. Они «подкатываются» к доминанте-квинте, чтобы утвердить на ней новую тонику.
Как это может происходить?
Если бы мы захотели запечатлеть этот процесс модуляций с помощью ключей-клавиш клавиатуры…
Впрочем, посмотри на страничках ниже. Вот что у нас получилось бы. Башня! В целых две страницы. Довольно громоздкая геометрия.
Геометрия нотной записи, конечно же, выглядит компактнее.
Две страницы (которые ниже) упаковались, сжались в две строки.
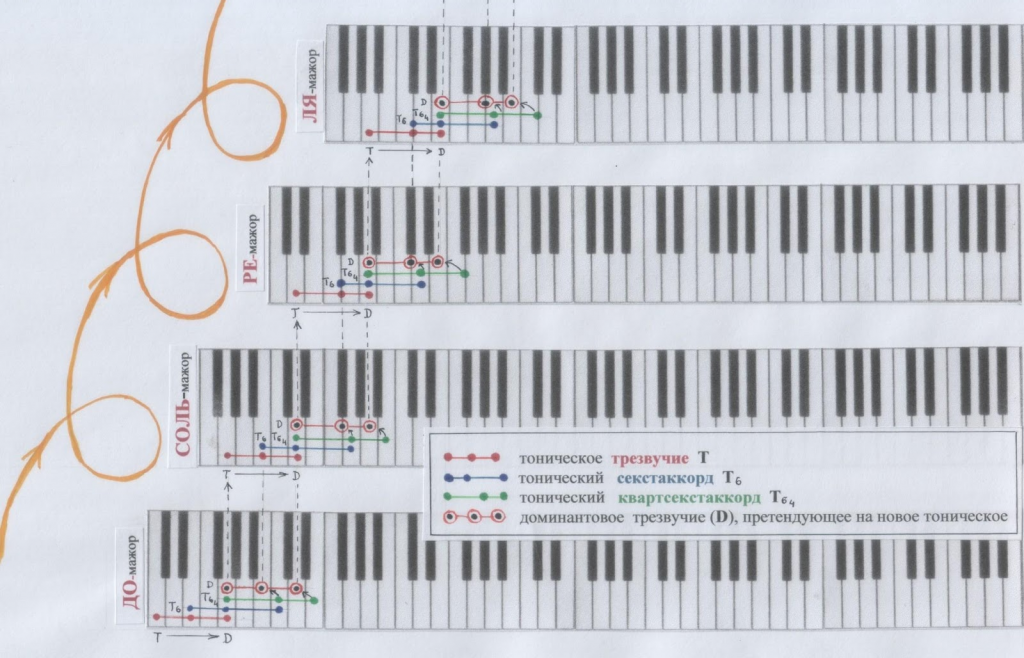
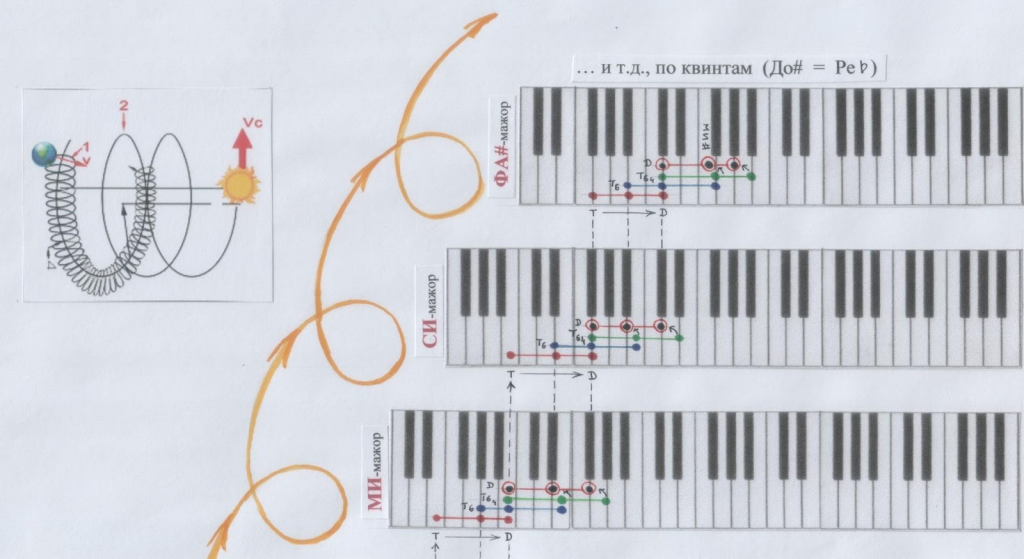
/Рис. автора. Вверху справа – рис. из Интернет источника в свободном доступе/
Как в данном случае происходит модуляция по квинтам?
Тоническое трезвучие, обернувшись квартсекстаккордом, оказывается на доминантном звуке (на квинте). И тут срабатывает гравитация, притяжение, «магнитное поле» доминанты. И эта доминанта перетягивает верхнюю терцию тонического квартсекстаккорда к себе поближе и превращается в новое трезвучие, с новой тоникой.
Сила притяжения звуков! Эта сила и связывает, и влечёт к переменам.
Эта сила – соль модуляций.
А гравитацию-притяжение создаёт о б щ и й з в у к (объединяющий звук).
Мы можем поиграть в модуляции по квинтам и в миноре.
Правда, в натуральном миноре доминанты будут получаться не активными, а будто вялыми, несколько печальными. Или слишком спокойными? А может быть, слишком задумчивыми, погружёнными в себя? Во всяком случае, они не вспыхивают энергией солнечных лучей.
Ты можешь воспроизвести это на клавиатуре (читая нотные знаки) и услышать в звуках.
/Рисунки автора/
В г а р м о н и ч е с к о м миноре всё куда интереснее! Ведь там появляется
м а ж о р н о е доминантовое трезвучие. Есть возможность вообще уйти в мажорные тональности.
А можно возвращаться к минору. И тогда мажорный «всплеск» будет похож на улыбку посреди задумчивости, на лучик надежды посреди печали, на солнечный проблеск меж облаков, на лоскуток радуги во время дождя… Ты же помнишь, что хроматизмы – это оттенки: оттенки звука – как оттенки цвета. Гармонический минор – цветной!
/Рис. автора/
Круженье аккордовых звуков можно я в н о ощутить, если проиграть аккорды приёмом а р п е д ж и о (вспомнились арфа и кифара).
Ты, пожалуй, заметил, что размах (масштаб) темперированного строя никак не умещается в пространстве только скрипичного ключа.
А ничего удивительного. Темперированный строй, можно сказать, рос вместе с оргáном. Масштаб – ого!
Только подумаешь об оргáне – и тут же слышишь в себе его пронизывающие бездонные б а с ы. Пространство!
Басовый ключ явился нам так незаметно и естественно, лишь только мы пожелали прогуляться по пространству звука, по его квинтам.
Есть ли тайны у басового ключа?
Ключ «ФА».
Вот сразу покажу звуковой диапазон оргáна – нотными знаками:
/Рис. из Википедии./
Конечно, как же обойтись тут без басового ключа?
Но почему этот ключ – именно «ФА» (а не тоже «СОЛЬ», что на первый взгляд кажется более удобным)?
А мы вспомним про систему координат с «нулевой точкой отсчёта» — ДО Первой октавы – прямо напротив нашего сердца. Влево – НИЗ, вправо – ВЕРХ.
Мы выбираем систему отсчёта, чтобы с чего-то начать ориентироваться в пространстве. А дальше – начинаем сРАВНивать, исходим из РАВНости, РАВЕНства, РАВНОвесия.
Мы уже поняли, что в пространстве звука мерой является квинта (да и не только в мире звука, как попутно стало выясняться…).
Равновесие квинт справа и слева от ДО: справа вверху «СОЛЬ», слева внизу… «ФА». Равновесие квинт – вот и вся причина.
Но почему образы ключей «СОЛЬ» и «ФА» – их «печати» — так разнятся?
В тайную геометрию ключа «СОЛЬ» мы заглянули.
Правый узел, со всеми его скрытыми возможностями (может, и не со всеми, но кое-какими).
На самом деле тайны ключа «ФА» очень похожи на тайны ключа «СОЛЬ».
Мы можем приблизиться к их разгадке, начав с геометрии в пространстве.
На сей раз нам даже лента не понадобится. Достаточно воображения.
Этот ключ легко представить завитком ленты.
Пусть она следует правилам поведения звука.
Тогда она движется снизу вверх, охватывая ДО малой октавы, закручивается справа налево и завязывается узелком на ФА. Левый узел!
Его «жизненное пространство» — квинта линеек нотного стана для квинты пальцев левой руки.
И в пропорциях ключа есть квинтовые отношения:
Отношения кварты (отражения-перевёртыша квинты) в нём тоже можно обнаружить:
/Рисунки автора/
В последнем случае четыре линейки, занимаемые ключом, намекают на четыре ступени октавы, которые занимает кварта.
И намёк на такое знакомое До-мажорное трезвучие:
/Рис. автора/
Ключ «СОЛЬ» показывает нам его на линейках, а ключ «ФА» — в промежутках между линейками.
Почему так?
По-видимому, эти два ключа желают, чтобы мы о чём-то догадались. О чём-то весьма важном в нашем мире, о каком-то секретном его свойстве или принципе.
…Ч е р е д о в а н и е!
День и ночь (то Солнце, то Луна), бодрствование и сон, активность и покой, лето и зима, тепло и холод, уход и возвращение, вдох и выдох, высота и глубина, гребень волны и её провал, выпуклость и вогнутость, предметы (объём) и пространство (ёмкость для предметов).
Даже атомы в кристаллических решётках упаковываются чередованием:
/Рис. из книги: Л.Тарасов. Этот удивительно симметричный мир. М. Просвещение. 1982г./
А в нашем проволочном «еже» («по Фибоначчи») чередуются додекаэдры и икосаэдры.
В музыке чередуются сильные и слабые доли.
Ноты на нотном стане тоже «упаковываются» чередованием: на линейке – между линеек, на – между, на – между…
А в результате – вращательная симметрия пространства!..
(Или это вращательная симметрия – виновница чередования?)
Чередование и консонансы:
/Пометки автора/
Мы меняем точки зрения. Мы играем зрением ума. Мы находим подобия.
В темперированном строе терция по своей подобности квинте в трезвучии (до-до#-ре-ре#-ми, — это так, напоминание) тоже была причислена к консонансам, вместе со своим обращением – секстой.
Можем поиграть ещё. Например, в системе отсчёта, где мерой является интервал т о н (как расстояние, как шаг между звуками).
Обратим внимание на то, что в басовом ключе терция МИ-СОЛЬ выделена особенно (двумя точками) и дана в сравнении с узелком ФА.
МИ-ФА=1/2 тона, ФА-СОЛЬ= 1 тон; вместе – 112 тона (3/2).
ФА — м е ж д у МИ-СОЛЬ: 3/2:2=3/4. Число кварты.
Мы можем менять системы отсчёта, масштаб этих систем – и находить при этом подобия.
Так или иначе, но ключ «ФА» настойчиво указывает нам на перевёрнутую квинту (квинту вниз) – то есть на кварту.
Даже если мы затеем игру в модуляции по к в и н т а м вниз от «нулевой точки отсчёта» ДО, то обнаружим, что первым обращением основного трезвучия (ДО-МИ-СОЛЬ) у нас окажется КВАРТсекстаккорд (СОЛЬ-ДО-МИ).
А следующее обращение приведёт нас в мир б е м о л ь н ы х тональностей: начиная с Фа-мажора.
На клавиатуре это движение-вращение аккордов будет происходить справа налево (подражание левому узлу), а в нотной записи – сверху вниз.
Ты же всё это можешь проверить сам, экспериментально: читая то, что таят в себе кругленькие печати нот и отворяя путь звукам ключами-клавишами.
/Рисунки автора/
Низ – тяжесть. Тяжесть – плотность. Плотность – вещественность, предметность. Бемольные тональности мы воспринимаем как более веские, плотные, густые.
Диезные тональности, стремящиеся ввысь, — прозрачны, светлы, легки. Ключ «СОЛЬ», открывающий им ход вверх, — солнце.
Мы даже можем поиграть мыслью так:
— Всё, что «диезно», обладает свойствами пространства. Потому что – высь. Небо, свет, воздух. Тонкая материя мира, которую и материей-то не назовёшь. Потому говорим — п р о с т р а н с т в о. Мир атомов и субатомных частиц мы тоже мыслим как пространство, пространство-время. В нём кружат потоки неразделимые, пронизывающие друг друга. Пространство помогает лучше понять явление связности.
— То, что «бемольно» — подобно сгущению материи, уплотнению, утяжелению. Эти сгустки мы видим как п р е д м е т ы, обретающие
о т д е л ь н ы е ф о р м ы. Мир отдельных форм – это и есть дискретный мир. Мы не видим, что внутри него тоже существует связность (как связанность его атомов, которые являют собою волны). Мы видим отдельные формы предметов.
Наше познание мира начинается с познания этих отдельных форм. Из мира отдельных форм мы создаём фундамент познания. Это – наш «бас» ( база – бас).
Когда мы геометрически пытаемся представить себе модель с в я з н о с т и как связанности всего со всем, мы начинаем с построения того, что приведёт нас к Золотому сечению – этой всепронизывающей симметрии самоподобия. Мы начинаем с удвоенного к в а д р а т а, иначе – той же к в а р т ы ( и то и другое – «четыре»). Мы строим модуль-октаву с двумя квартами. Это – фундамент, «бас». Две точки басового ключа, похожие на знак деления, фиксируют ноту ФА – IV ступень («квадратную» ступень) в До-мажоре, этом «нулевом диапазоне отсчёта» в музыкальном строе. Деление – от/деление – отдельность. Они царят в мире телесных, вещественных форм. Когда мы приходим в мир, мы застаём его таким. С этого «баса»-фундамента и начинается наша жизнь в мире.
К пониманию связности всех отдельных форм мы приходим потом, вытягиваясь ввысь (мыслью, зрением ума в том числе), в вертикаль, к свету – подобно ключу «СОЛЬ», который утверждает квинту вверх, квинту-доминанту. Ключ «СОЛЬ» — намёк на доминантовую функцию (роль) в жизни и музыке. Ключ «ФА» и IV ступень в модуле-октаве связаны с функцией
С У Б д о м и н а н т ы.
На тему ДОМИНАНТЫ мы размышляли достаточно много и разносторонне.
А что такое СУБДОМИНАНТА? Какие смыслы в этом слове?
Энциклопедия:
СУБ… от лат. sub – «под».
Часть сложных слов, которая означает нахождение внизу.
Ещё она означает «внутрь» и «свёртывание».
И такой смысл: «основа».
Все эти смыслы нам уже приоткрыли себя в размышлении о квартах в модуле-октаве и о басовом ключе.
Смыслы «под» и «низ»:
Любая тональность (ТОНАЛЬНОСТЬ) являет нам себя в форме модуля-октавы. В октаве есть квинта вверх – доминанта, V ступень. И есть квинта вниз – IV ступень, кварта. Октава развивается по законам движения звука (обертонов) – снизу вверх. На клавиатуре – слева направо. По высоте звуков кварта (IV) – под квинтой (V), внизу.
Смыслы «внутрь» и «свёртывание»:
Доминанта – это развёртывание (вспомним о вращательной симметрии пространства). Развёртывание мы мыслим как движение слева направо, снизу вверх. Квинта снизу вверх. Развёртывание – выход в пространство.
Субдоминанта – противоположность развёртыванию. Свёртывание, уплотнение. Мы это мыслим как движение сверху вниз, справа налево. Квинта-перевёртыш – ход в плотно-материальный мир, вещественный мир, предметный.
Но этот мир – наша основа, фундамент, «бас». Вот и последний смысл – «основа».
Функции внутри ТОНАЛЬНОСТИ развиваются так:
ТОНИКА – выбранная система отсчёта. – СУБДОМИНАНТА – веская основа. – ДОМИНАНТА – высшее проявление, выход в пространство, ввысь. С возможностью перемены системы отсчёта. – ТОНИКА – возвращение в начальную систему отсчёта. Схема: T – S – D – T.
/Рис. автора/
СВЯЗНОСТЬ. Связанность ключей,
Был ли ты внимателен?
Был ли ты достаточно внимателен, когда аккорды кружились перед твоими глазами на нотном стане, взбираясь по квинтам вверх и спускаясь по квинтам вниз?
Чем заканчивалось их круженье ты помнишь?
Может ли вообще заканчиваться круженье?
Хорошо, что летучие звуки можно запечатлевать нотами. У нас всегда есть возможность вернуть промелькнувшие мгновенья и внимательно их изучить, промыслить.
Смотри сейчас на «концовки» модуляций:
Мажоры. Диезные снизу вверх и бемольные сверху вниз.
Миноры. Диезные снизу вверх и бемольные сверху вниз.
/Рисунки автора/
Что происходит?
А происходит то, что мы наблюдаем прелюбопытнейшее явление.
Тональности могут превращаться!
Они могут обращаться так же, как и трезвучия. Они могут вращаться и изменять свой образ: диезные – на бемольный образ, бемольные – на диезный. Они поступают так же, как и квинты, да и вообще как все интервалы. Вращательная симметрия пространства!
Тебе знакомо выражение «о с л е п и т е л ь н ы й свет»? Но мы знаем, что слепота – это тьма.
Когда свет становится нестерпимо ярким, мы прикрываем веки. Когда насыщенность светлых диезов зашкаливает в тональностях, наступает поворот к усмирению их активности бемолями. Когда бемоли погружают тональности в глухую тьму, является вспышка диезного света. Этим и космос держится.
Если наша мысль сейчас и дальше продолжит модулировать, заразившись энергетикой модулирующих тональностей, она может сделать удивительное открытие. Каждая тональность может содержать в себе и диезные свойства и бемольные! Вопрос только в том, какие свойства в ней возобладают в какой-то момент, в каком конкретном образе она тогда предстанет. Но мы ведь тоже предстаём в разных образах в течение нашей жизни или даже одного дня, даже одной минуты…
Темперированный строй, словно под увеличительным стеклом, дал нам возможность увидеть в нотах и ощутить в звучании это удивительное явление противоположностей в одном (2 в 1) и поочерёдное доминантное проявление этих противоположностей.
Круженье-преображение тональностей обычно изображают в виде Квинтового круга тональностей.
Просто посмотри картинки на следующих страницах.
/Рис. из книги: Вахромеев В.А. Элементарная теория музыки. М. Музыка, 2007г. Пометки автора./
/Пометки автора/
/Рис. из книги: Вахромеев В.А. Элементарная теория музыки. М. Музыка, 2007г. Пометки автора./
/Пометки автора/
Ты обратил внимание на то, что в «точках» ДО и ЛЯ словно происходит перекрёст кругов? — Очень похоже на склейку в ленте Мёбиуса или перекрёст ленты при завязывании узла.
А вообще в музыке для этого явления существует специальный термин:
э н г а р м о н и з м.
Это только на первый взгляд термин отпугивающе непонятный. Но зрение ума ведь не раз приводило нас в глубины смыслов всяких терминов, — и смыслы озарялись светом понимания.
Энциклопедия:
Энгармонизм – от греч. en – «в» («внутри») и harmonia – гармония.
Гармония – со/звучие, со/существование в со/гласии.
В ТОНАЛЬНОСТИ могут сосуществовать два возможных её проявления: бемольное и диезное. Тональность внутри тональности.
Бемольное проявление – к НИЗУ, плотности, плоти, сгущению, затемнённости. Диезное – к ВЫСИ, пространству, свету.
Как и мы: то в заботах земных ( о теле и его комфорте), то в душевных порывах ввысь, к духу, умозрениям всяким… Но при этом мы остаёмся собою. С двумя возможностями проявлений себя. К тому же эти возможности мы можем проявлять «мажорно» и «минорно» («мажор» — «большой», «минор» — «малый»; разный размах, масштаб, мера активности…).
Энгармонизм позволяет быстро и даже неожиданно поменять направление модуляций – от бемольного к диезному и наоборот. Ведь любую бемольную тональность можно тут же превратить в диезную, а диезную в бемольную, — что заставит трезвучия вращаться по-новому, в новых направлениях. Достаточно вдруг увидеть новым взглядом за бемолями диезы, а за диезами – бемоли.
Обязаны ли бемольные тональности быть привязанными только к направлению ВНИЗ, а диезные – к направлению ВВЕРХ?
Вовсе нет!
Любое земное дело можно делать с душой и смыслом. Это возвышает земные заботы. Так домостроительство превращается в искусство архитектуры, заботы о еде – в искусство кулинарии, заботы о комфорте – в искусную инженерию и т.п. Высокие замыслы – продукты наук и искусств – воплощаются, реализуются в предметах, которые делают наше земное существование более комфортным и исполненным красоты.
В космосе тёмную материю пронизывают фотоны, а в центрах сияющих галактик – сверхплотные чёрные дыры…
В каждом человеке – женские и мужские гормоны (вещества, определяющие пол; дело в том, какие «победили»).
Взаимопроникновение противоположностей.
Хорошо знакомая всем и ныне невероятно популярная древнекитайская эмблема-символ – об этом.
Вот и бемольные тональности могут подниматься ввысь, по о б р а т н ы м квинтам (обращённым), иначе – по квартам:
А диезные тональности могут спускаться вниз, тоже по квартам:
/Рисунки автора/
Если ты проявил любопытство экспериментатора и проиграл всё это на пианино, у тебя, скорее всего, могло возникнуть чувство какого-то несовершенства, незавершённости: словно модуляции не совсем настоящие, переход в тональности слишком быстрый и зыбкий, — не успеваешь его ощутить. Может быть, в данном случае не хватает второго обращения трезвучия?
Как бы там ни было, но в музыке субдоминантовая функция, которая связана с квартой, используется именно для передачи ощущения незавершённости в музыкальном предложении.Когда предложение оканчивается неопределённо, с сомнением, такое окончание называют н е с о в е р ш е н н ы м кадансом (от лат. cado – «оканчиваюсь»).
Кварты у нас вообще показывают равновесие в октаве. Они не желают выходить за её пределы. А значит, и в тональности они будут «голосовать» за старую добрую Тонику. Субдоминантовая функция кварт – за неё. Ну могут кварты-Субдоминанты «выглянуть в окошко» другой тональности, однако предпочтут остаться дома, к Тонике поближе:
И даже в этом примере ты ещё не услышишь окончательного совершенства. Потому что… как же без Доминанты? Зачем тогда и в окошко выглядывать, если не манят бескрайние просторы, само бесконечное пространство, — воздух, солнечный свет, космическое небо?.. С квинт-Доминант и жизнь-то начинается! Да, у нас есть дом, но мы выходим из него – чтобы вернуться.
Получается что-то вроде этого:
/Рисунки автора/
Модуль-октава и функциональный модуль нашей жизни.
Здесь вот что интересно: появление в аккорде доминантовой функции того же звука, что и в тональности, в которую мы «выглянули в окошко» (из Фа в Си-бемоль). Этот звук устанавливает связь с поманившей тональностью (Си-бемоль). Но он возможен только если доминантовая функция явится нам не трезвучием, а четырёхзвучием (ДО-МИ-СОЛЬ-СИ-бемоль и его обращения).
Можно говорить и «четырезвучие» (так у Римского-Корсакова).
Есть один важный нюанс в обращениях четырезвучий. В этих обращениях появляется д и с с о н а н с – интервал с е к у н д а (она же – обращённая септима по краям начального аккорда).
А как же не появиться этому диссонансному настроению?! – Мир манит, а тебе велено – домой! Квинты-доминанты рождены для бесконечности, а тут – конец свободе. О г р а н и ч е н и е, границы. Отдельность, отделённость от бесконечности. Вот она, дискретность. Так велит модуль-октава. И вписанная в этот модуль ТОНАЛЬНОСТЬ. Мир отделённых друг от друга форм. Мы ведь, телесно, — тоже отдельная форма. Лишь мысль странствует бесконечно.
Человеческая мысль добралась и до космических бездн, а жить нам – на Земле.
Хотя… Пространство проникает в нас беспрестанно. Мы вдыхаем воздух ( вдыхаем небо! его кислород – в каждом нашем сосуде, в каждой клеточке ), наши тела – по большей части вода (а для многих земных существ она – пространство жизни), магнитные потоки пронизывают нас. Мы не видим этого круженья, этой связности, но что же это, если не квинты-доминанты?
Совершенство непременно требует доминант связности даже в дискретных формах. Сложно?
А в модуле-октаве всё это есть. И в каждой тональности это есть. И мы столько раз это видели! И слышали!
Ещё чуть-чуть об аккордах.
Да, выходит, что они бывают не только трезвучиями, но и четырезвучиями. И даже пятизвучиями. Шестизвучия не принято использовать. Они при вращении-обращении производят слишком много диссонансов – хаос.
Итак: три – четыре – пять.
Три эти числа и ограничивают возможности аккордов.
Тебе эти числа ничего не напоминают? – Например, из математики, из геометрии…
/Рис. автора/
Египетский треугольник – дитя окружности, поделённой на 12 частей.
Египетский треугольник, имеющий связь с Золотым сечением, с квинтами.
?
Опять эта симметрия самоподобия проникает всюду. И ведёт к вращательной симметрии пространства…
Пятизвучие называют нонаккордом, потому что оно вписывается в интервал нону.
Четырезвучие называют септаккордом, потому что оно вписывается в интервал септиму.
По аналогии трезвучие хочется назвать квинтаккордом, потому что оно вписывается в квинту. Но его так не принято называть. Можно перепутать с квинтсекст-аккордом, обращением септаккорда, четырезвучия.
Просто основное трезвучие. И всё.
Оно может явиться нам в виде четырёх звуков: ДО-МИ-СОЛЬ-ДО. Но всё равно останется трезвучием, так как его прима и октавный звук – по сути, один и тот же звук, только удвоенный. Поскольку такое трезвучие охватывает всю октаву, его называют полным тоническим трезвучием.
Когда музыкальное предложение заканчивается тоническим трезвучием, мы слышим совершенный каданс (или совершенную каденцию).
Всё согласовалось: модуль-октава, в этом модуле – тональность, в тональности – главные функции: тоника Т – субдоминанта S – доминанта D – и возвращение в тонику T. Полнота проявлений земного и небесного, предметного и пространственного миров, дискретность и связанность. Совершенство!
Вот интересно, если ТОНАЛЬНОСТЬ не решится поддаться смелым призывам Доминанты отправиться в головокружительную бесконечность по квинтам со сменой своих образов, а предпочтёт всё-таки остаться дома, в своём модуле-октаве — поддавшись влиянию Субдоминанты (субдоминантовой функции), которая всегда за Тонику, за стабильность, — будет ли у неё при этом возможность изменяться, модулировать?
Я думаю, что мы похожи (мы с ТОНАЛЬНОСТЬЮ). Знаешь, чем? – Внутренним сходством. Мы можем изменяться в н у т р и себя, то есть тоже модулировать, но исходя из своих внутренних ресурсов, разных способностей.
У всех живых существ способности зашифрованы в генах.
(Ты, наверное, знаешь в общих чертах, что гены – это такие вещественные образования в нашем организме, которые в определённом порядке упаковываются в другое красивое вещественное образование в виде двойной спирали под названием ДНК, а ДНК упаковывается в хромосомы, те – в ядра клеток, а из клеток состоим мы.)
Гены передаются нам по наследству, от родственников (греч. γένοζ – «род»).
У любой тональности всегда найдётся как минимум шесть ближайших родственников, чьи гены в неё упакованы (как у нас ближайшие шесть родственников: мама, папа, две бабушки, два дедушки).
(Это страничка из чудесной и умной книги, написанной всемирно известным русским композитором Николаем Андреевичем Римским-Корсаковым. Называется эта книга «Практический учебник гармонии». Этот учебник написан для студентов Санкт-Петербургской консерватории, но написан так ясно, что при желании любой пытливый ум сумеет постичь смысл его содержания.)
Строями Р.-К (Римский-Корсаков) называет тональности. Названия мажоров пишутся с прописных букв (больших, мажорных), а названия миноров – со строчных букв (малых, минорных).
Помещена эта страничка в раздел «Модуляция».
Приведённые примеры показывают, что практически каждый звук октавы-тональности готов проявить себя как родственная тональность со своей неповторимой особенностью-способностью. Каждый музыкальный ген может прийти в активное состояние, и тогда основная тональность, изначальная, почувствует в себе изменение – то есть осуществление модуляции. Какие «гены» будут активированы и задействованы – зависит от неповторимой мелодии. Как применять определённые аккорды для гармонизации мелодии – об этом тоже пишет в своём учебнике Р.-К.
Мелодия влечёт за собою и модуляции в родственные тональности.
И эти модуляции тоже происходят благодаря способности аккордов вращаться-обращаться, связывая между собою нужные тональности.
Не обязательно будут задействованы в с е возможные тональности, нет.
Неповторимая мелодия изольётся из души и сделает выбор.
В этом есть свобода и непредсказуемость.
Но есть и правила взаимоотношений между Тоникой, Субдоминантой и Доминантой в тональности – распределение функций, обязанностей согласования действий. Как же совместить свободу и непредсказуемость с правилами поведения?
Есть один секрет.
Он заключается в том, что к а ж д ы й аккорд каждой родственной тональности присоединяется к Субдоминанте или Доминанте, тем самым выражая своё согласие исполнять их функции ( Тоника в данном случае – главная, а речь – о родственниках): удерживать поближе к Тонике (Субдоминанта) или осуществлять порыв к новизне, к выходу за пределы (Доминанта).
Субдоминантовую функцию исполняет, во-первых, сама же Субдоминанта (аккорд IV ступени). А к ней присоединяются и начинают исполнять её роль аккорды (а соответственно, и тональности) II и VI ступеней.
Например, в До-мажоре – это ре-минор и ля-минор.
На основании чего это они решили присоединиться именно к Субдоминанте?
А по закону тяготения, притяжения, гравитации. Их притягивают друг к другу общие звуки:
Видишь, у Субдоминанты довольно прочные связи с Тоникой. Именно Тоника тонического трезвучия их взаимно притягивает.
У Доминанты тоже есть связь с тоническим трезвучием, но… с его квинтой.
А квинта, мы знаем, всегда может увлечь в дальний путь без пределов…
Доминант-септаккорд с его обращениями возвращает к Тонике. Однако Доминанта всегда остаётся неустойчивой.
/Рисунки автора/
Все подробности о правилах поведения «родственников» главной тональности, их взаимных связях при модуляциях ты можешь узнать из того же «Практического учебника гармонии». Эти правила строги, как законы физики и математики, но удивительным образом они способствуют рождению невероятного числа таких непохожих произведений!
К слову, мы ведь тоже неповторимы, несмотря на действие общих для нас законов физики и генетики…
Думаю, тебя несколько удивит необычное расположение аккордов в примерах из учебника. Звуки этих аккордов раскинулись по гигантским вертикалям, на всё пространство обоих ключей.
/Рис. из книги: Римский-Корсаков Н.А. Практический учебник гармонии. М., ЛИБРОКОМ, 2017г./
Зачем так?
…Оргáнный масштаб: тысячеголосый хор флейт, — п р о с т р а н с т в о,
много пространства для дыхания тысяч труб, для свободного полёта звуков с их обертонами. Каждому звуку аккорда есть место развернуть с в о ю мелодию, и эти мелодии, встречаясь, связываясь друг с другом, сольются в новые аккорды… Полифония – многозвучие, многоголосие. Римский-Корсаков звукам аккордов даёт имена человеческих голосов. Снизу вверх (по правилам поведения звука): бас, тенор, альт, сопрано.
Когда мы поём, мы выдыхаем воздух-пространство; когда поёт оргáн, его трубы тоже выдыхают воздух-пространство.
Трудно на первый взгляд распознать порядок в этих разбросанных звуках, и тем удивительнее его обнаруживать – обнаруживать связанность звуков. Так удивительно, наверное, открывать связанность звёзд в космических безднах силами гравитации, общей сетью… Когда попривыкнешь ориентироваться, даже захватывает дух от открывающихся возможностей.
А сами ключи? Это же всё происходит в их владениях – всё это связанное непрерывное круженье-звучание. Как бы они удерживали всё это в своей власти, не будучи сами связанными?
Давай экспериментировать! Думать и экспериментировать.
Вернёмся к геометрии в пространстве. Вспомним, что басовый ключ у нас – левый узел (вяжется справа налево, по движению линии ключа), а скрипичный ключ – правый узел (получился в результате эксперимента).
Левый узел — ключ «ФА» — показывает квинту влево (на клавиатуре); правый узел – ключ «СОЛЬ» — показывает квинту вправо (тоже на клавиатуре). Место их встречи, или их общее начало, — ДО.
Мы можем представить себе отношения «ФА» и «СОЛЬ» в системе координат:
Конечно, мы подразумеваем, что где-то между ними «нулевая точка отсчёта» ДО. Но ведь в музыкальной системе, которая измеряет пространство-время не точками, а квинтами (самых разных масштабов), ДО измеряется тою же мерой. ДО – квинта вверх по отношению к ФА и квинта вниз по отношению к СОЛЬ. Относительность в действии! У ДО двойная роль: + и —, бемоль-диез в наложении друг на друга. В результате – нейтралитет. Вот смысл её «нуля». Если промоделировать это квинтами-узлами, они неизбежно выведут нас из прямоугольной системы координат, существующей на плоскости, в пространство. Вот как узлы покажут смысл ДО:
Слияние узлов
/Рисунки автора/
Остаётся довершить это стремление к соединению:
/Модели автора/
Оказавшись на свободе в пространстве, эта фигура продемонстрирует свойства ленты Мёбиуса: закольцованная бесконечность, в которой два сливаются в одно – две поверхности становятся одной, и, двигаясь в одном направлении, подобно звуку и Времени, мы охватываем две противоположности – низ и верх (глубину и высоту, «что было» и «что будет»).
К этому волшебству ты можешь прикоснуться, сделав эту простенькую модель.
Это волшебство двух ключей.
Какая же «печать» в нотной записи запечатлевает его?
О, она тебе так хорошо знакома, что ты, наверняка, даже не замечаешь её, когда открываешь ноты.
Акколада – от франц. accolade – «объятие».
Тактовая черта, «пульсируя» на протяжении всего музыкального произведения, беспрестанно напоминает нам об акколаде-объятии.
А вот ключи и акколада в виде непрерывности, связанности:
/Пометки автора/
Просто забавный рисунок из Интернета, симметрия нашего сердца (из книги И.И.Шафрановского «Симметрия в природе») и «Мёбиус» наших сосудов (из Атласа анатомии человека), – где даёт о себе знать пульс-Время:
