Тетрадь 5
/Авторский коллаж на основе рисунков из Интернет источников в свободном доступе./
Жизнь.
Жизнь была дальше.
И музыка-жизнь.
В жизни – эволюция.
Эволюция – это перемены, и з м е н е н и я форм вещей и существ. То же, что м о д у л я ц и и (ты же помнишь, что модуляция – это закономерное и з м е н е н и е).
Маленькие клеточки-точки объединяются во всё более сложные формы.
Если интересно, — Энциклопедия всегда готова прояснить любую мысль:
Эволюция — от лат. evolutio – «развёртывание», закономерное изменение.
Развёртывание – это укрупнение: малое превращается (модулирует) в большее, но в соответствии с общими и для малого и для большого законами.
Изменения в космосе, изменения на Земле.
Простенькие атомы водорода «развернулись» в сложную Таблицу Менделеева. Космическая пыль – в галактики. Клеточки жизни – в homo sapiens (человека разумного).
Маленькие государства-города древней Греции (полисы) «развёртывались» в империи (империя Александра Македонского, затем – Римская империя).
Силы множественных греческих богов «развернулись» в мощь единого Бога, Всемогущего.
Музыка жаждала мощи, силы, величины. Или Величия.
Струна – тонка. Она нежно ударяет по воздуху, и тот долетает до нашего слуха подобно ласкающему ветерку. Звук лёгкий, изысканный,— для тонкого душевного (психейного) внутреннего нашего мира. Очень личный голос.
Личность, её душа, её отдельная мелодия – вот что может выразить струна.
А множество мелодий могут ли, объединившись,«развернуться» в единую мощь? Даже множество струн выразят ли её?
Пространство-время, изменяясь, искало для выражения себя новый голос.
Хор. Множество голосов, усиливающих друг друга. Не соло души, а мощный единый дух.
И… труба!
И… аккорд!
Вот что было нужно.
Отвергнутая когда-то Афиной флейта Пана требовала своего возрождения. Она желала возродиться вновь, но уже в новом обличье.
Греческое слово pan означает «всё». Греческий Пан был богом, который подчиняет себе множественность: бог пастухов и их стад; бог лесов со всем многообразием населяющих их существ. Его флейта имела силу подчинять своим звукам множество жизней, объединять их силы в единую мощь.
Афина же отдавала предпочтение героям-личностям, личному человеческому духу и миру души. Она отдала предпочтение струнной кифаре.
Но пришло время флейт.
Звук флейты пронзителен и прям. Воздух, сжимаясь в её трубе, вылетает подобно стреле или снаряду и ударяет по нашим барабанным перепонкам напрямую (не опосредованно, как от колебаний струны).
Струна растягивается и сжимается, колеблется; звук кружится и растекается волнами. Флейта непоколебима. Жестка и прямолинейна. Её длину и диаметр не изменишь в процессе игры. Раз отрезал – и всё.
Флейта требовала фиксации звуковых высот, их точности – в соответствии с точным расчётом своих параметров. Её отверстия для регуляции воздушного потока должны точно соответствовать определённым высотам звуков (да и сами они похожи на точки).
Энциклопедия:
Фиксация – от лат. fixus – «закреплённый».
/Рис. из Википедии/
Греки отличались пытливым умом и изобретательностью.
Они явили миру инструмент, который можно было бы назвать «суперфлейтой» (гиперфлейтой) Пана.
Гидравлос!
228г. н.э.
Изобретатель – древнегреческий математик и механик Ктесибий.
Это такая водяная флейта, или водяной орган.
Вот тебе и эволюция – «развёртывание» идеи флейты до масштабов органа!
Более подробная информация – на следующей странице.
/Источник – Википедия/
Гидравлос – довольно сложное механическое сооружение. Оно именно
м е х а н и ч е с к о е. Управлять звуком непосредственно (как к струнам – непосредственно прикасаясь чуткими пальцами) на нём просто невозможно.
Разве можно было на нём передать всё богатство звуковых красок пифагорова строя (36 звуков-оттенков!)?
Звуковые оттенки, которые давали микрооктавные интервалы в пифагоровой октаве, наверняка пришлось упростить.
Но зато появилась сила звучания. Эта сила – сильнее человеческого голоса.
Сила нашего голоса зависит от силы наших лёгких, от их мощности.
С помощью наших лёгких мы можем надуть воздушный шарик. А велосипедную шину, к примеру?
Насос куда мощнее наших лёгких!
В гидравлосе был применён насос.
Богатство звуковых оттенков было принесено в жертву силе звучания. Этой силы должно было хватать на покорение слуха сотен и тысяч собиравшихся вместе слушателей.
Как музыканты управлялись с гидравлосом? – Так сразу не поверишь: ударом кулака! И колотили они по специальным дощечкам шириной 5-7 см, устроенным на горизонтальной панели. Вот эти дощечки и получили название: К Л А В И Ш И.
Откуда взялось это слово – КЛАВИША?
— От латинского слова clavis – «КЛЮЧ».
Почему «КЛЮЧ»?
Да потому что ключ открывает и закрывает вход-выход.
В случае с гидравлосом клавиши были связаны с клапанами, которые открывали и закрывали вход-выход для воздушного потока в трубах.
Стукнул по нужной клавише – и полетели волны воздушного давления к нашим ушам, чтобы наш мозг превратил их в звук.
Разные трубы – разные волны – разные звуки.
Вот можешь полюбоваться на первую клавиатуру:
/Рис. из книги: М.К.Инал-ипа (Хотелашвили). Орган. Краткий исторический очерк./
На этой клавиатуре ещё нет знакомых нам чёрных клавиш. Все клавиши – одинаковы. Что бы это значило?
(Очень жаль, что на фото греческого гидравлоса не видно клавиатуры. Но орган из древнего города Аквинкум в бывшей провинции Римской империи – на территории современной Венгрии — наследует сам принцип устроения греческого инструмента.)
Почему все клавиши одинаковы?
На какой музыкальный строй они намекают?
На этом инструменте 13 клавиш (посчитай сам). На греческом – 24.
По-видимому, нам опять придётся прогуляться на Восток – к вавилонянам, шумерам и… в Китай. К вавилонянам и шумерам прогуливался и Пифагор, и другие его соотечественники. А вот Китай…
Каким-то образом шумерская и вавилонская цивилизации пересекались в древности с китайской цивилизацией – ещё более древней, чем шумерская. Кто у кого заимствовал всяческие премудрости – до сих пор остаётся загадкой: то ли китайцы учились у шумеров, то ли шумеры – у китайцев… Но известно, что в Китае существовала очень-очень древняя музыкальная система, разработанная для… флейт! И кем? –Опять же – а с т р о н о м а м и!
Эта система называлась «Система 12 люй».
(Если пожелаешь познакомиться с этой системой обстоятельно, знай, что есть такой сайт www.synologia.ru Музыкальная теория.)
Так вот, иероглиф люй буквально означает «правило», «устав». В музыке – это система звуковысотных эталонов (так написано в статье на сайте). То есть система из образцов высоты каждого звука – эталонов этих звуков.
Страницей ниже (так, на всякий случай) – отрывок из статьи.
Всё очень просто. Как у шумеров и египтян. Пространство-время планеты Земля в космосе измеряется вращением по окружности: 360 «шагов» (градусов) – 360 дней года; год – из 12-ти месяцев. Каждому месяцу соответствует звук определённой высоты. Образуются звуки в соответствии с лестницей квинт (тебе это знакомо по пифагоровому строю). Только эта лестница поделена на одинаковые ступени, по половине тона. Каждому звуку – по ступеньке: 12 звуков – 12 ступеней. По-нашему это будет так:
I ступень – ДО VII ступень – ФА диез
II ступень – ДО диез VIII ступень — СОЛЬ
III ступень – РЕ IX ступень – СОЛЬ диез
IV ступень – РЕ диез X ступень — ЛЯ
V ступень – МИ XI ступень – СИ бемоль
VI ступень – ФА XII ступень – СИ
Как китайцы получили эти звуки?
— Из квинт! Опять-таки из квинт.
Ну что поделать, если квинты – это доминанты, то есть высшее проявление силы, а значит, и выразительности (или выраженности) каких-то явлений – энергии, волны, например: гребень волны, её кульминация, импульс. А весь мир – из волн (как мы уже понимаем).
Эти доминантовые кульминации (импульсы) показаны в фильме «Вселенная. Звуки космоса» из нашей первой тетради. Они представлены как звуки новорождённой Вселенной, которым больше 13 миллиардов лет. Это происходит на в о с ь м о й минуте фильма. Ты ведь можешь пересмотреть этот фрагмент.
С этих доминантовых импульсов и началось то, что я в и л о с ь,
с т а л о б ы т ь, то есть сам мир, сама жизнь.
Посмотри на ленту из квинт с привычными названиями нот ( не умею писать иероглифы, а ты не умеешь их читать):
Здесь все необходимые звуки для всех 12-ти ступеней.
Они окажутся рядом, если мы свернём эту ленту спиралью и учтём, что не закрашенные карандашом ноты – это подобия тех вертикалей ступеней, которые мы получали в строе Пифагора: то есть мы будем шагать через одну квинту, и постепенно у нас выстроится весь ХРОМАТИЧЕСКИЙ китайский звукоряд.
(Эту спираль найдёшь на следующей странице.)
Так что выходит, что ХРОМАТИЧЕСКИЙ звукоряд – родом из Китая.
Хроматический – значит, построенный по полутонам.
Однако само название «хроматический» — от греческого слова chromatos –«цвет», «окраска».
Греки вообще мыслили звуки цветными: семь звуков гаммы (гептатоники) подобны семи цветам радуги. А каждый полутоновый звук подобен оттенку: ФА – цвет, ФА диез – оттенок ФА… и т.д.
По-гречески, весь звукоряд состоял бы из лимм.
/Модели автора/
В случае с флейтами такой звукоряд был очень удобен. Трубы есть трубы, чем проще – тем лучше.
Конечно, и в таком звукоряде есть октава. Стóит лишь добавить 13-ю ступень, подобную первой ступени, но на новом витке.
Дело только в том, что китайцы не мыслили и н т е р в а л а м и – отрезками, в которые вписываются звуковые волны, не мыслили звуки в о т н о ш е н и и друг к другу, — то есть никакого принципа относительности.
Тем более удивительно, что их строй оказался совместим с пифагоровой октавой.
А может, и НЕ удивительно: ведь оба строя сотворены из одних и тех же «атомов» — квинт.
Зачем трубам относительность? Фиксированный звук (зафиксированная, эталонная его высота) – вот и всё, что нужно трубам. Фиксированный размер трубы – фиксированный звук.
Для гидравлоса, первого оргáна — первого духового механического инструмента – такой строй вполне подходил.
Слово оргáн – тоже греческого происхождения (греки изобрели, греки и назвали). Происходит оно от слова οργανον (органон) – «орудие», «инструмент», «машина».
Вот что сообщает Энциклопедия по поводу оргáна:
Оргáн – крупный музыкальный духовой х р о м а т и ч е с к и й
клавишный инструмент с мехами, трубами для извлечения звука.
Вот! Х р о м а т и ч е с к и й инструмент. Вот почему количество клавиш первых оргáнов – в соответствии с хроматическим строем. Вот почему все клавиши – одинаковы, «равны». Как равны полутоны.
Однако не всё было так просто с этим хроматическим строем, как кажется на первый взгляд.
Мы-то знаем теперь, что звуковые волны ведут себя в соответствии с астрономическими особенностями поведения Земли в космосе, между Солнцем и Луной. Пространство-время Земли задаёт её годовой поворот не в 360˚, а в 365˚ (или 366˚). Поделить этот поворот (виток спирали на самом деле) на р а в н ы е 12 частей не получается. А значит, какие-то из этих частей не будут подчиняться равенству, и 13-й полутон не повторит в точности первый ( а это – звук октавы). Потому Пифагор и ввёл к о м м у, микроинтервал-разницу.
Китайцы просто две части из двенадцати чуть изменяли. На слух это было не очень заметно. Ведь духовые инструменты предназначались для игры на открытом воздухе, где воздушные волны быстро рассеиваются, и уши не успевают разницу уловить. Тем более, если исполнять только м е л о д и и –
п о с л е д о в а т е л ь н ы е звуки.
Первые оргáны ( те самые гидравлосы с небольшим количеством труб) тоже использовались для больших праздников на открытом воздухе.
Оргáны покоряли Европу. Сила их звучания очень даже соответствовала имперскому духу (Римская империя), духу Величия.
Да, оргáн – это е в р о п е й с к и й инструмент. И китайские хроматизмы-полутоны постепенно вживились в древнегреческий строй (Греция ведь – Европа), в пифагорову октаву. Для этого пришлось пожертвовать микроинтервалами.
Та клавиатура, которую мы знаем, и демонстрирует нам этот процесс вживления полутонов-хроматизмов в октаву Пифагора.
Пифагорову октаву взялись представлять собой белые клавиши, среди которых сохранились два естественных полутона: МИ-ФА, СИ-ДО.
Мы можем проследить этот процесс образования нового строя. Его показывают клавиши. А клавиши, мы теперь знаем, это – КЛЮЧИ. Ключи, которые открывают путь не только потокам воздуха и волнам звука, но и волнам МЫСЛИ, понимания.
Это ты увидишь на странице ниже.
/Рис. автора/
Благодаря клавишам-ключам октаву теперь можно было не только услышать, но и у в и д е т ь. Ещё её можно было о с я з а т ь, прикасаться к ней.
Сам порядок мира (такой неуловимый, незримый) можно было «взять в руки», исследовать его, испытывать его свойства – и на слух, и на взгляд, и на ощупь одновременно. Играя клавишами-ключами, мир можно было
м о д е л и р о в а т ь, создавая бессчётное число моделей жизни (которые впоследствии стали называться пьесами, этюдами, сонатами и т.д. – муз. произведениями).
«Китайский след» в европейской октаве (изначально – пифагоровой) ты можешь увидеть, услышать и осязать, постукивая своими молоточками-пальцами по чёрным клавишам. Ты услышишь китайские наигрыши. Ты услышишь п е н т а т о н и к у («пента» — «пять», «тон» — «звук»). Играя ключами чёрных клавиш, ты можешь моделировать какие-то «наброски», мелодии жизни «по-китайски» (как будто на китайском языке).
Устойчивое отношение «3» и «2» (тернарность и бинарность, троичность и двоичность) навсегда впечаталось в клавиатуру:
И это всё – след КВИНТЫ.
О т н о ш е н и е трёх к двум и двух к трём — след пифагорова «струнного» подхода, волнового подхода: частоты и длины в о л н. И – и н т е р в а л ы.
С у м м а ( последовательное присоединение фиксированный значений):
3+2=5 — квинта в виде зафиксированных звуков-ступеней ( квинта ведь – пятая ступень в октаве). «Флейтовый» подход, сущность которого – зафиксированная высота звука.
Геометрический символ этого – пентаграмма, которая была священна и в древнейшей китайской культуре, и священна для Ордена пифагорейцев.
(Интересно, что разгадать загадку устойчивости сочетаний «3» и «2» не получается (до сих пор!) даже у современной физики.
В поисках самой малой частицы мироздания – на субатомном уровне – физики добрались до к в а р к о в. И выяснилось, что получить о д и н кварк невозможно. Они связаны какими-то гиперсильными силами в пары или тройки. И чем большую силу прилагают, чтобы разъединить эти пары и тройки, тем крепче кварки сцепливаются друг с другом !
А числа, которыми описывают свойства кварков, словно позаимствованы из музыкального строя.)
Какие же невероятные возможности открывал оргáн для музыки, для моделирования жизни из волн (волн звука)!
Флейт (труб) можно было использовать любое количество.
Количество струн ограничено небольшими размерами рамы самой лиры (или арфы). А трубами можно уставить хоть стадион! Лишь бы клавиатуры хватило.
И что же стало?
Оргáн превратился в архитектурное сооружение!
Архитектурное сооружение из тысяч труб (бывших флейт).
3 тысячи, 4 тысячи. …33тысячи труб!
Самый гигантский и самый мощный по силе звука оргáн был построен в 1929-1932г.г. в Америке, в Атлантик-Сити (штат Нью-Джерси). 33 112 труб!
Вот это развёртывание идеи оргáна! Даже за пределы Европы, через Атлантику. И за пределы человеческого слухового диапазона: утверждают, что трубы этого гиганта могут воспроизводить инфразвуки и приближаться к ультразвукам.
…Но мы вернёмся пока что в Европу.
Посмотри на эволюцию человеческой Мысли, её модуляции – в картинках.
/Рисунки из Интернет источников в свободном доступе/
/Рисунки из Интернет источников в свободном доступе, вверху – с пометками автора,/
/Рис. из Интернет истолчников в свободном доступе./
Да, пифагорова ОКТАВА стала проще. В ней сохранились только главные консонансы – прима, октава, квинта и её перевёртыш кварта. Они зафиксировались ступенями: I, VIII(I), V, IV. Круженье микрозвуков (микроинтервалов) будто распрямилось в линейку полутонов, похожих на фиксированные точки/звуки.
Но зато ОКТАВУ-модуль можно было переносить вправо-влево, по высоте звуков – вверх-вниз. От «точки отсчёта» — первой октавы.
Словно система координат Декарта.
А «точкой отсчёта» является октава, которая соответствует среднему человеческому голосу (петь в первой октаве умеют все!). И, кроме того, она всегда располагается прямо напротив нас: МЫ – ОКТАВА, зеркально.
А дальше можно двигаться хоть в бесконечность!
Мы уже пробовали представить себе бесконечную клавиатуру для бесконечных волн звука и его модуляций (звук-ультразвук-инфразвук-радиоволны-элктромагнитные колебания…).
Но даже бесконечность наших мыслей, их волны-ленты мы упаковываем в буквы-точки и печатные строки. Мануалы оргáна похожи на строки в книгах, на раскрывающиеся книжные страницы…
Для того чтобы все модули-октавы сцепливались друг с другом, «склеивались», в с е звуки «через октаву» должны были звучать согласованно, точно, без колебаний вроде коммы – как в окружности совпадают начало и конец (а комма, если помнишь, свидетельствует о спирали,— в которой начало и конец не совпадают).
Нужно было найти какой-то максимально ТОЧНЫЙ, фиксированный очень ОПРЕДЕЛЁННО, коэффициент отношений между в с е м и звуками.
Вот и начались м а т е м а т и ч е с к и е эксперименты и теории.
Математики становились теоретиками музыки, музыканты-композиторы – тоже теоретиками и математиками.
Математиков (а все они в какой-то мере – наследники Пифагора по духу) будоражила мысль о «живом» Числе – т.е. о Числе, которое моделирует саму Жизнь через пропорции, отношения; это пифагорово волшебство превращения бесплотного неощутимого Числа в реальный ощутимый звук, в волны, из которых творится дыхание жизни.
Музыкантам-композиторам нужны были неограниченные возможности инструментов и новых средств для выражения этого дыхания, для переполнявших их души чувств и мыслей.
Что их так волновало?
— Захватывающая идея и захватывающий процесс под названием ТЕМПЕРАЦИЯ!
Энциклопедия:
Темперация – от лат. temperatio – правильное соотношение.
(Не могу удержаться от комментария посреди энциклопедической статьи. В этом слове – «темперация» — сошлись два смысла: temp (время, или пространство-время) и ratio (разум, рассудок). Разумное упорядочивание пространства-времени звука: ведь сама природа звука связана с природой земного времени.)
В музыке темперация – это выравнивание интервальных соотношений между ступенями.
Темперацией занимался и Пифагор, создавая свой строй. Выравнивать интервальные соотношения помогало изменение натяжения струны и особое устроение кифары, позволявшее корректировать звуки прямо в процессе исполнения. Но в записи эта темперация предстаёт неравномерной.
Попытки перенести пифагорову струнную темперацию на флейты только подчеркнули неравномерность изначальных расчётов строя Пифагором, без этой струнной коррекции.
«Система 12 люй» приближала к решению проблемы – через полутоновые соотношения. Но проблему коммы эта система не решала.
(Интересно, что китайцы, рассчитывая свой строй, с флейтами поступали аналогично тому, как Пифагор со струной на монохорде, — когда определял основные консонансы.
Они, грубо говоря, брали трубу и нарезáли её на отрезки разной длины, которые становились флейтами. Высота звука зависела от длины отрезка трубы.
Взяли кусок – он стал изначальным тоном (примой). Отрéзали от него 1/3. Получили 2/3. Он зазвучал как квинта.
А дальше к октаве они стали подбираться через квинты (квинтовые шаги, или квинтовые ходы).
Отрезок с первой полученной квинтой они опять брали за основу и уже от него отрезáли 1/3. И так поступали до тех пор, пока не добирались до октавного звука. А это получалось через 12 шагов (операций отрезáния). Длина флейты уменьшáлась – звук становился выше.
Если длину трубы брали на 1/3 больше изначальной, звук становился ниже и звучал как кварта – ¾. Из кварт можно было получать звуки с понижением.
И всё было бы замечательно, если бы получаемый в конце концов октавный звук в точности согласовывался с примой. Но этого не получалось, — как и у Пифагора при изначальном делении струны.
/Ой-ой-ой, прости, пожалуйста, ещё на мгновение отвлечёмся. Вот тебя прямо сейчас не озарила одна изумительная мысль в связи с китайскими флейтами? – Ведь сам принцип фрактальной геометрии – он же
ф л е й т о в ы й !!! Берёшь отрезок, вычитаешь 1/3; из каждого полученного отрезка опять вычитаешь 1/3, и опять повторяешь эту же операцию, и опять… — Это же квинтовые шаги! Все фрактальные фигуры образуются квинтовыми шагами. Эту операцию с отрезками проделывали и Кох, и Серпинский, и Мандельброт… Фракталы = музыка?! Фрактальная геометрия – родом из музыки, а значит, и из астрономии?.. Ну и сюрпризы способен преподносить нам мир и модуляции Мысли!../)
Да… Европейцы столкнулись с проблемой неравномерной темперации строя в связи с оргáнами. Любопытно, что вначале они тоже пошли по «китайскому пути», пытаясь вычислить высоты полутонов. И тоже пришли к десяти одинаковым полутонам и двум отличающимся по высоте, но тоже равным.
Этими вычислениями занимался немецкий математик и теоретик музыки Генрих Граммáтеус (1492-1525гг.). Он повторил китайцев в расчёте полутонов.
Следующий шаг совершил итальянский теоретик музыки и композитор Винченцо Галилеи (1520-1591гг.), отец знаменитого астронома Галилео Галилея.
Из статьи о нём в Википедии: «В настройке лютни он предлагал делить октаву одинаковыми полутонами 18:17 — эта величина, хотя и рассчитанная приблизительно, весьма близка равномерно темперированному полутону.»
Зачем нужны были р а в н ы е отношения между звуками, зачем нужна была одинаковая м е р а отношений между их высотами (один и тот же коэффициент) и почему именно оргáн потребовал этого?
Тысячи труб – это тысячи звуков.
Это – невероятные возможности проявления мощи звучания.
Это – великий соблазн создать грандиозную модель грандиозного мира: Вселенная-Земля-Человек с его душой и духом. Соблазн смоделировать такую сложную Жизнь, в которой, тем не менее, всё как-то согласуется, — причём в к а ж д ы й м о м е н т существования мира.
Вот если бы в мысленном эксперименте «Жизнь» мы в какое-то мгновенье нажали клавишу «стоп» (как на компьютере во время кинофильма), мы бы увидели о д н о в р е м е н н о е сочетание всех движений всех существ и явлений, попавших в «кадр», — словно замерли, зафиксировались отдельные ноты мелодий их жизней (в масштабе Вселенной – жизней планет, звёзд, галактик…). Мы бы увидели что-то, похожее на аккорд.
Мы бы увидели, что в каких-то точках все сложные движения согласуются, не мешают друг другу и даже вторят друг другу, — и тем поддерживают друг друга. Они оказались в моменте к о н с о н а н с а. Они словно упорядочивают множество всех, таких разных, движений, — которые кажутся нам на первый взгляд сплошным хаосом.
В хаосе есть точки, которые и не согласовываются друг с другом – диссонансы. Они рассеяны, не согласованы друг с другом. В них нет силы. Сила проявляется в согласованности.
Сила аккорда – в согласованности его звуков-точек, в г а р м о н и и.
Мир не рассыпается в пыль хаоса благодаря консонансам.
Слова «точка» и «точный» — родственники.
Чем точнее консонансы – тем большей силой они обладают.
Фиксированные звуки флейт, ставших трубами оргáна, и желание самогó пространства-времени, желание самой Жизни явить себя в аккордах – совпали.
Каждый звук должен был иметь шанс поучаствовать в аккорде: ведь все они рождены квинтой-доминантой. Шансы у всех звуков должны были быть р а в н ы. Один и тот же коэффициент отношений между звуками устанавливал это равенство.
Так и явилась в мир музыкальных звуков идея р а в н о м е р н о й
т е м п е р а ц и и всего музыкального строя.
Как ни странно, задачку с этой самой равномерной темперацией (причём, точнее всех) решил человек, на родине которого и не помышляли об оргáне. Соотечественников этого гения вовсе даже и не интересовали его эксперименты и расчёты. Заинтересовали только 200 лет спустя.
Чжу Цзай-юй.
Нам уже встречалось это имя.
Он был современником Винченцо Галилея ( Винченцо Галилей: 1520-1591гг., Чжу Цзай-юй: 1536-1610гг.).
Так в одном информационном поле Земли о д н о в р е м е н н о вспыхнули импульсы-озарения Мысли европейской и китайской. Им оставалось только окончательно слиться в консонансе.
Но кто такой Чжу Цзай-юй?
— Учёный, астроном, математик, лингвист и музыковед, изобретатель музыкальной темперации.
Так представляет его нам Энциклопедия.
Интернет может более обстоятельно познакомить тебя с его биографией – если, конечно, возникнет к этому интерес.
А ещё он был человеком сильного духа.
Когда его отца, принца по рождению, жившего во дворце, оклеветал завистливый родственник, возжелавший занять высокое положение при императорском дворе, в результате чего отец оказался в тюрьме, 14-летний Чжу Цзай-юй ушёл из дворца и поселился в землянке. Не впасть в уныние ему помогла страстная любовь к наукам, — чем он и занялся в своём уединении.
Оргáн он, естественно, не мог построить в своей землянке. Но в его распоряжении были флейты и струнный инструмент цитра.
Древнюю китайскую «Систему 12 люй» (для флейт) он изучил очень досконально. С пифагоровой системой (для струн) наверняка тоже был знаком. (Китай давно установил торговые отношения со странами Средиземноморья через Шёлковый путь, а потом – морской.) Оставалось сравнить эти две системы, найти в них то общее, что их объединяет, и… привести их к консонансу.
А общим у этих систем было их астрономическое и математическое происхождение. Только подход к природе звука отличался. У флейт – звук-точка, у струн – звук-волна.
(С подобной двойственностью столкнулись европейские учёные-физики 16-18 веков, когда изучали природу света. Англичанин Исаак Ньютон остался приверженцем корпускулярной теории: свет (фотон) – есть частица-корпускула («точка»), правда, со свойствами волны. Англичанин Томас Юнг доказал, что свет – волна, и даже измерил длины световых волн. А вместе получилась корпускулярно-волновая теория.)
Чжу Цзай-юй создавал «флейтово-струнную» теорию музыкального строя (тоже в своём роде корпускулярно-волновую (не в строгом смысле, конечно, а по подобию), — для звуков).
Пифагорову комму он решил р а в н о м е р н о распределить на все 12 люй (до их повторения на новом витке), а по сути – на 12 квинт (ведь все люй образуются квинтами) и точно зафиксировать полученные высоты звуков. Для этого ему надо было точно рассчитать длины флейтовых труб, — с учётом распределённой между ними коммы.
Это примерно то же, что 365 земных суток разместить в 360 (365˚ в 360˚).
Спираль замкнуть в кольцо, — как мы ощущаем время земного года: всегда с возвратом в одну и ту же точку (Новый год).
Солнечно-лунная пифагорова комма равномерно «растеклась» по 12-ти квинтам (как по 12-ти месяцам земного года). Квинты зазвучали в соответствии с числом 122.
Чжу Цзай-юй нашёл своих очень заинтересованных сторонников не в родном Китае, а в далёкой Европе.
Там над темперацией трудились знаменитые математики – голландец Симон Стевин и француз Марен Мерсенн. Они всё ещё искали свои варианты, как и композитор Андреас Веркмейстер, вдохновлявший И.-С. Баха. Но всё-таки равномерно темперированный строй Чжу Цзац-юя одержал верх. Наверное, из-за своей универсальности. Этот строй стал международным.
…Ты же помнишь, что мы начали эту тетрадь с темы эволюции – то есть «развёртывания» жизни.
Равномерно темперированный строй и стал именно р а з в ё р т ы в а н и е м.
Развёртыванием чего? – Да октавы же!
И тоже – по подобию.
Вот Пифагор с в е р н у л октаву, чтобы получить м и к р о -звуки, виновница которых – комма. Он показал, что подобия уводят в микро-мир, мир тонких материй и энергий, в мир волн и колебаний.
А темперированный строй показал иное подобие. Подобие в сторону увеличения.
Ступень обычной октавы развернулась величиной в саму октаву и, прошагав семь шагов-октав (подобно семи ступеням гаммы-гептатоники), стала величиной в клавиатуру. (Можешь проверить на своей клавиатуре.)
Каждый полутон обычной октавы стал подобием квинты этой же октавы. И 12 этих квинт уместились в семи октавах, — как 12 хроматических ступеней в гамме.
В общем, твоя клавиатура – это огромное подобие октавы (гамма + «хвостик» из оставшихся звуков).
Если к клавиатуре-октаве прибавить ещё одну, и ещё одну, и ещё… — доберёмся до вселенских масштабов!.. Это же мечта оргáна!
Клавиатуры оргáнных мануалов отдают дань особого почтения квинте, этой прародительнице жизни: количество октав каждого мануала – 5, как правило. Но мануалы некоторых оргáнов могут иметь и 5, и 7 октав, — выражая почтение и квинте, и гептатонике (гамме). Музыкальный строй ведь содержит и то и другое.
Если учесть ещё и педаль (ножную клавиатуру) в две октавы с «хвостиком», то в особо величественном оргáне всего октав наберётся от 33 до 37.
То есть, космическому замыслу пифагорова строя оргáн дал развёрнутый – просто гигантский! – масштаб. Представляешь, — каждому из 36-ти звуков и микро-звуков – разворот величиной в целую октаву!
А как же это космическое круженье, которое так прекрасно моделировала струнная кифара? Доступно ли его передать жёстким флейтам-трубам?
О, как изощрённы бывают модуляции человеческой Мысли!
Разрастаясь («развёртываясь»), оргáн покинул поля, где властвовал Пан. Тысячи труб нуждались в особо экономной «упаковке» (как природа экономно «упаковывает» атомы в молекулах и кристаллических решётках сложных образований – веществ, клеток…).
Вариантов этих «упаковок» столько, сколько и самих оргáнов (ты видел на картинках). Они стали архитектурными «организмами». И, как и любой организм, они нуждались в защитной оболочке.
Самой подходящей защитой оказались храмы.
У слова «храм» столько смысловых модуляций – ой-ой-ой!
Самый простой смысл – «дом», наша охрана в жизни. Да и само слово звучит очень близко к «хран» — охрана.
Вариант этого слова – «хорóмы», от «хорóм». Вот в этом варианте появляется смысл «хор» и его модуляция – «гор», гора. Хор – это общность множества голосов, приведённых к согласованности, гармонии:
согласованность человеческих мелодий жизни, а в более широком смысле – жизней всех «тварей» («творений»), населяющих Вселенную. «Гор», «гора» — высота, взлёт, кульминация, доминанта жизни, высшее проявление её сил.
В английском варианте храм – temple. В этом слове намёк на Время в вариациях его быстроты: пространство-время разных скоростей жизни разных творений Вселенной – во взаимной согласованности.
Какие музыкальные смыслы!
Геометрический смысл – куб и сфера: куб самого тела храма, а на сферичность указывает купол. (В проекции на плоскости – это квадрат и круг, и, может быть, намёк на бесконечность известной нам «квадратуры круга». А может быть, «прямоугольное круженье»…)
Вселенная из звуков, помещённая в эту охранную оболочку, стала вести себя в соответствии с моделью настоящей вселенной. Круженье вернулось. Как? – Во многом благодаря полусфере купола.
Звук любит полёт. Звуковые волны охотнее всего взлетают в высоту (всем известно, что звук от источника внизу лучше прослушивается вверху, а не на уровне источника). А вверху – сферическая поверхность купола. Вот и завихриваются о т р а ж е н и я звуковых потоков, и обволакивают нас. И может закружиться голова – как от звуков кифары.
А ещё палитра звуков оргáна развёртывает себя в ТЕМБРАХ.
Слово тембр происходит от франц. timbre, от греч. timbanon (timpanon) – «ударять». В теории звука означает «качество звука». А качество (характер) звука зависит от призвуков, обертонов, сопровождающих основной звук. А особенности призвуков зависят от ф о р м ы колебаний источника звука. А эта форма колебаний зависит от качеств материала, из которого сделан источник звука (шероховатая или гладкая форма, жёсткая или мягкая…).
Трубы оргáна сделаны из дерева и металла: одни – из дерева, другие – из металла. У деревянных труб – тембр мягкий, бархатистый, глубокий, обволакивающий. У металлических труб – тембр жёсткий, гладкий, пронзительный. Однако, металл подбирается для труб мягкий: сплав олова и свинца – чтобы звуки, обладая силой металла, не резали при этом слух.
Просто неизмеримое количество звуков может творить оргáн – и впрямь хватит на все творения Вселенной.
Слушая оргáн в храме (или концертном зале с хорошо рассчитанными отражательными свойствами – как в храме), мы оказываемся посреди круженья.
Тональности, шагая по квинтам вверх и вниз, тоже кружат.
Всё – как в космосе.
Само пространство-время кружит в музыке. И всё изобилие звуков (с их обертонами и отражениями) , которое может сотворять оргáн, представало бы хаосом, если бы не закон консонансов – совпадений, согласований, созвучий: гармонии.
Чем больше звуков, тем больше они нуждаются в организации – гармонизации, тем сильнее должна проявлять себя власть гармонии.
Вот эту силу и власть гармонии и дал АККОРД!
Аккорд непременно должен был родиться. Настало его время.
Чтобы понять, как это произошло, давай кое-что припомним о самой природе звука – с помощью картинок. Они – на следующих страницах.
/Рисунки из Интернет источника: статья Звук и акустика, Энциклопедия Кругосвет; из книги: А.Г.Белявский. Теория звука в приложении к музыке. Лекции 1921г./
Вот если бы мы могли у в и д е т ь круженье звуков, круженье звуковых волн, когда звучит орган под куполом храма…
Мы бы у в и д е л и, как возникают моменты согласования между какими-то звуками среди многих, и это согласие объединяет и усиливает мощь этих звуков. Если бы мы остановили такой момент, чтоб у в и д е т ь…
Знаешь, в книге К.Пиковера «Великая математика» меня поразила одна картинка, невероятно похожая на такой момент. Странная Сфера Александера…
Она вся – словно из вдруг явившихся взору и замерших витков многочисленных спиралей потоков (воздуха? звуков?).
Это именно м а т е м а т и ч е с к и й объект, созданный американским математиком Джеймсом Александером. И этот объект называется с ф е р о й, потому что обладает важным геометрическим свойством сферы – непрерывностью. Он п о д о б е н сфере. ( В книге употреблено выражение «гомеоморфен сфере»: греч. homoios – «подобный», morphe – «форма». То есть, этот объект и сфера — п о д о б н ы е формы по свойству непрерывности.)
Этот объект, если приглядишься, бесконечно воспроизводит п о д о б и я самого себя. А ведь это – принцип и музыкального строя!
Вначале на картинке не очень понятно, чтó происходит, кáк всё это организуется. И вдруг… Начинаешь видеть точки (узлы), которые находятся в согласовании друг с другом!
Следующие страницы нашей тетради предлагают тебе у в и д е т ь это удивительное явление согласования ( гармонии, консонансов), которое проступает в кажущемся (на первый взгляд) хаосе.
/Из книги: К.Пиковер.Великая математика.М. БИНОМ, Лаборатория знаний, 2015г./
Сферу моделируют смыкающиеся-размыкающиеся пальцы – большой и указательный.
/Осн. Рисунок – из книги К.Пиковера Великая математика. М. БИНОМ, 2015г. Пометки автора/
/Осн рисунок из книги: К.Пиковер. Великая математика. М. БИНОМ, Лаборатория знаний., 2015г.Пометки автора/
То, что мы увидели, математиками называется ф р а к т а л о м.
Фрактал – родственник Золотого сечения.
Поразительный момент: формат самóй книжной картинки позволили измерить «аккорд» обыкновенной линейкой. И линейка показала при этом числовые меры Ряда Фибоначчи…
Ещё одной интересной особенностью представшего нам объекта является то, что кольца витков р а з о м к н у т ы (пример с пальцами, приводимый К.Пиковером в статье к картинке) – как в случае с витками спирали: каждый виток спирали – разомкнутое кольцо. И очередное подобие фигуры образуется в месте размыкания. Такое явление нам уже встречалось:
/Рис. автора/
Как непохожи все эти фигуры: Сфера Александера, обыкновенная сфера, пентаграмма. А музыку вообще невозможно у в и д е т ь.
Но все эти явления родственны, п о д о б н ы, потому что сам принцип их организации – с а м о п о д о б и е.
И аккорды тоже рождены в мир этим принципом.
Если изобразить звуковые пространственные волны на плоскости (как мы привыкли их себе представлять), то среди множества волн совпадающие по одной линии гребни-кульминации и явят нам аккорд.
/Рис.из статьи Звук и акустика. Интернет Энциклопедия Кругосвет. Пометки автора./
Наше умозрение аккорд видит как в е р т и к а л ь посреди звуковых потоков. Аккорд упорядочивает эти потоки силой своей вертикали. Он – сила. В музыкальном пространстве-времени он совпадает с сильной долей.
В музыке архитектуры он предстаёт колонной. И тогда он подобен древнегреческому Атланту, который весь порядок небесных сфер держит на своих плечах.
Если подумать о природе и о Древе Жизни, аккорд – ствол этого Древа.
Корень Древа подобен глубокому гулкому басу, основанию. Волнующаяся листва кроны – мелодии…
Бас – сокровище оргáна. Его гул похож на бездну и на незримый, но весомый и плотный, центр гравитации. Никакой иной музыкальный инструмент не владеет этим сокровищем – не по силам! Великан один лишь может…
Реликтовое излучение – бас Вселенной. Центры галактик, их опоры – бас. Он – первый тон в основании ТОНАЛЬНОСТИ (какие бы образы эта «актриса» ни принимала). В мире космического круженья он тоже подчиняется закону квинт-доминант. Только поступь его облечена особым Величием.
/Рис. автора/
БАС — АККОРД — МЕЛОДИЯ.
Вот триада, моделирующая пространство-время в звуках.
Науки и искусства изобретают свои особенные термины для феноменов (явлений) мира, в которых про/являются его законы.
На первый взгляд ( или слух) термины запутанны, как хаос, непонятны, а потому скучны. Пока не проникнешь в их живое сердце…
Вот, например, такой «запутанный», сложный, многословный термин:
«ГОМОФОННО – ГАРМОНИЧЕСКИЙ СКЛАД».
…Но ведь у нас с тобой уже есть опыт проникновения в самое сердце терминов зрением ума.
«СКЛАД» — это понятно: складывать – прилаживать что-то друг к другу, прикладывать, упорядочивать – порядок.
«ГАРМОНИЧЕСКИЙ» — от «гармония»: консонансы, согласованность; в концентрированном проявлении – аккорд.
«ГОМОФОННЫЙ»…
Здесь нам и понадобится применить опыт проникновения зрением ума. В сердце, в корень. Вернее, в корни этого слова.
Греч. phone –«звук».
Лат. homo – «человек». Греч. homos – «равный», «взаимный», «общий».
Вместе – «человеческий звук»: голос, мелодия. Звук, общий человеческому голосу и своей собственной природе – непрерывной волне.
В переводе на более понятный музыкальный язык мы получим в результате: «МЕЛОДИКО – АККОРДОВЫЙ ПОРЯДОК (СТРОЙ)».
Вот когда употребляют термин «гомофонно-гармонический склад», то имеют в виду эту стройную триаду: БАС – АККОРД – МЕЛОДИЯ.
Это — о б о б щ ё н н а я модель мира в звуках.
Обобщённая – значит, без подробностей, без определённых мер, — в отличие от подробно рассчитанной октавы. Но при всём при этом геометрия даёт нам возможность увидеть, что обе эти модели – п о д о б н ы.
Только обобщённая модель, как и любое обобщение, выглядит величественнее.
Величие оргáна и востребовало утверждения такой грандиозной обобщённой модели. А р а в н о м е р н а я т е м п е р а ц и я посодействовала её созданию.
Бас – это центр гравитации (подобный центру галактики на наших картинках). Он утверждает себя как ТОНИКА – фундаментальный ТОН, фундамент, основание ТОНАЛЬНОСТИ – на какую бы квинту он ни взошёл.
Вместе с собою он переносит и модуль ОКТАВУ, внутри которой и рождается очередная ТОНАЛЬНОСТЬ со всеми своими АККОРДАМИ и МЕЛОДИЯМИ.
Бас тоже кружит по квинтам. Так центр нашей галактики (вместе с самóю галактикой) летит по какой-то гигантской спирали – к созвездию Геркулеса.
И тональности-времена жизни, возникающие на этом великом пути квинт, изменяются, м о д у л и р у ю т, обновляются.
И сама наша, человеческая, МЫСЛЬ кружит во Вселенной в соответствии с этой грандиозной моделью, — открывая ф у н д а м е н т а л ь н ы е законы мира (например, фундаментальные законы физики нашего мира), своды-аккорды законов в разделах наук (на примере физики – законы поведения твёрдых тел, жидкостей, газов, света, атомных и субатомных частиц и т.д.) и «мелодии» — линии развития этих наук во времени.
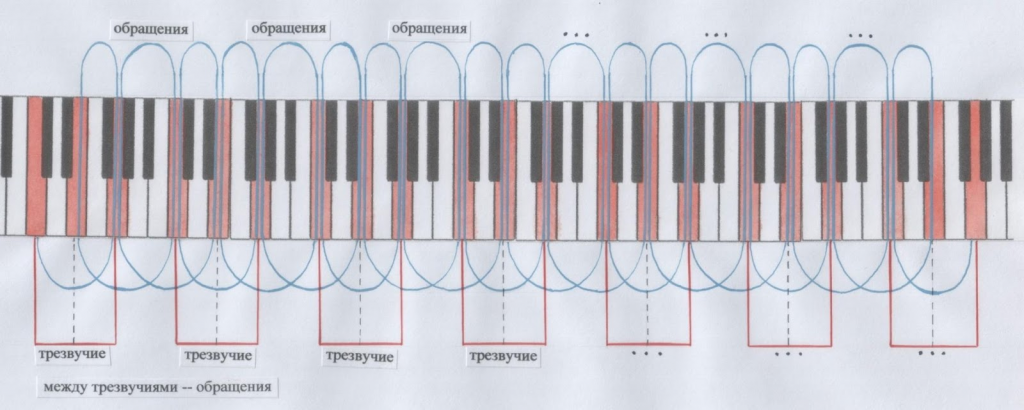
Аккорды в музыке – это моменты-импульсы совпадения, согласования нескольких импульсов (сильных проявлений) вращающихся звуков. Эти совпадения предстают перед нами как вертикаль, выстроившаяся в момент, когда мы этому вращению сказали «стоп» (мысленный такой эксперимент). В такой момент мы можем обнаружить, что звуки аккордов тоже вращаются. Иначе говорят, что они о б р а щ а ю т с я.
Тогда триада-трезвучие предстаёт перед нами в новых своих образах. Слово «обращение» соединяет в себе два смысла: «вращение» и «образ». Как ТОНАЛЬНОСТЬ является нам в образах разных (различающихся) тональностей, так и АККОРД – в разных образах. – Принцип подобия!
Чтобы увидеть этот сказочный процесс (в сказках ведь персонажи всё время обращаются в кого-то другого, — оставаясь при этом собою), воспользуемся ключами понимания – клавишами.
Итак, — образы-обращения триады (трезвучия):
/Рис. автора/
А может ли быть т р е т ь е обращение?
Клавиши показывают, что – да. Конечно, — да.
И оно возвращает нас к начальному трезвучию, но на новом витке, в новой октаве.
Это подобно тому, как начальный звук-прима превращается в октавный звук, образуя интервал ОКТАВУ. Октавный звук повторяет приму на новом витке спирали восхождения. Он – словно отражение примы.
Трезвучие повторяет себя своим третьим обращением – по принципу образования этого октавного звука – и получает своё отражение в новой октаве.
И всё повторяется снова и снова – до бесконечности. Лишь бы хватило клавиатуры…
Вот и само слово «повторение» — от «второй». Два. Характеристики октавного звука: 2 – частота волны, ½ — длина волны.
Третье обращение повторяет начало. «3» и «2» неразделимы в явлении вращения. Взаимоотношения «3» и «2» указывают на квинту: 3/2 – частота волны, 2/3 – длина; 5-я ступень в гамме и октаве (3+2). Трезвучие вписывается в квинту внутри октавы, само же своими хроматическими звуками повторяет октаву (смотри комментарии к картинке со Сферой Александера). Как всё взаимосвязано! …Потому что – п о д о б н о.
/Рис. автора/
/Рис. автора/
/Рис. автора/
