Тетрадь 2
/Авторский коллаж на основе фото Алексея Павленко (www/fotokto.ru) и картинок из Интернет источников в свободном доступе./
…История о молотках и наковальнях.
Эта история должна быть тебе знакома.
В связи с именем одного гения. Тоже тебе знакомого.
?
…Все рождённые люди имеют уши и мозг.
Пифагор был рождённым человеком. Следовательно, у него тоже были уши и мозг.
Замечательные уши!
Гениальный мозг!
2,5 тысячи лет (уже даже больше) тому назад, проходя мимо кузни медников, гениальный человек с замечательными ушами впервые (вот! «стать как новое утро в незнакомой стране») услышал нечто у д и в и т е л ь н о е…
Что?!
Он услышал… КОНСОНАНС!
Все слышали шум, звон, грохот. А он – КОНСОНАНС…
?
На самом деле Пифагор услышал то, что древние греки называли словом … «симфония». Это слово для них означало то же, что для нас французское слово «консонанс».
Энциклопедия:
Консонанс – франц. consonance, от лат. consonantia – созвучие, согласное звучание.
В древнегреческом – συμφωνία (simfonia: sim — «со», phone – «звук»; со-звучие). Слияние в восприятии одновременно звучащих тонов, или сами созвучия (интервалы, аккорды).
То есть определённые молотки медников при ударении (тон – «ударение») могли производить согласованные звуковые волны – созвучия, довольно приятные на слух, гармоничные.
Вот неизвестно, умело ли умозрение Пифагора увидеть внутри себя звук в виде волны, но поразительно то, что услышав молотки, этот человек догадался смоделировать волновой процесс (звуковую волну) с помощью колеблющейся струны!
Колеблющаяся струна стала первой вещественной моделью звуковой волны! Осознавал ли это Пифагор?
Что он сопоставил (соразмерил)?
Масса молотка – масса струны (масса куска струны, отрезка; сам кусок струны, отрезок) – сила, напряжение звукового тона (ударения).
Массивнее струна (длиннее) – меньше колеблется/напрягается – ниже звук.
Короче струна (меньше масса) – чаще колеблется/напрягается – выше звук.
(Как сердечки маленьких животных больше напрягаются, чаще бьются.)
От длины струны (её массы: массы куска меди, вытянутого в струну) зависит частота её колебаний/напряжений, высота тона.
Можно найти пропорцию (соразмерность) между длиной струны и высотой (напряжением) тона.
(В нынешней физике длине струны аналогична длина волны (в т.ч. звуковой волны); высоте/напряжению тона аналогична ч а с т о т а колебаний волны: чаще колеблется – больше напрягается.)
Гармоничные созвучия можно конкретно измерить! – Вот что привело Пифагора в восторг.
Невидимое, неуловимое, неосязаемое – можно измерить!
И тут же был изобретён измерительный прибор для вычисления звуковой гармонии – м о н о х о р д.
М о н о х о р д – от греч. monos – «один», «единый» и chorde – «струна».
Да, так просто: одна струна – измерительный прибор!
Точнее, одна струна, закреплённая на ящике. Струна определённой промеренной длины. И к струне – зажим, которым можно пережимать струну в любом месте, меняя тем самым тон её звучания.
Этот прибор многие годы служил ученикам Пифагора учебным пособием для изучения великого таинства ГАРМОНИИ. Не только в музыке!
Энциклопедия:
ГАРМОНИЯ: от греч. harmonia – «связь», «стройность», «соразмерность». Соразмерность частей, слияние различных компонентов чего-либо в единое органичное целое. В древне-греческой философии – организованность космоса («космос» — «красота») , в противоположность хаосу (греч. haos – беспредельная беспорядочная первобытная масса чего-то неопределённого).
Ого! Вот что происходит, когда обыкновенные и всем привычные звуковые волны попадают в уши гения. – Они модулируют, превращаясь в волны Мысли! Звук – музыка – философия. Вот это модуляция! (Философия – от греч. phileo – «люблю» и sophia – «мудрость»; любовь к мудрости.)
Музыка и космос. Весь мир! Этот мир сотворяется, организуется, существует благодаря с о р а з м е р н о с т и, согласованности — «созвучию» своих частей. Что согласовалось, «склеилось»,— то и обрело существование. Гармония – «клей» мира.
…Ты уже догадался, что ГАРМОНИЯ и КОНСОНАНС – это фактически одно и то же?
Но есть нюансы применения этих терминов. ГАРМОНИЯ – термин, который применим ко в с е м у миру, его устроению. И, соответственно, применим к музыке как части этого мира. А КОНСОНАНС – термин, который применяют, когда речь идёт о проявлении гармонии в м у з ы к е. Когда говорят о созвучиях м у з ы к а л ь н ы х звуков. Древние греки называли консонансы г а р м о н и к а м и. «Симфонии» — гармоники. У греков.
… Ещё не запутался?
/Просто вставка. Для общего сведения./
Но нужно понять: пифагорейцы музыку м ы с л и л и как космос. Они музыку м ы с л и л и как весь мир.
Мыслили и измеряли. Соразмеряли.
С помощью своего измерительного прибора – монохорда.
Вспомним: струна монохорда – что-то вроде вещественной модели звуковой волны.
Всё, что проделывал Пифагор со струной, описал его ученик Архит. Тоже великий учёный-мыслитель.
…Если ударить по натянутой струне (как по наковальне) молоточком или ущипнуть её, колебания этой струны мы услышим как ТОН («ударение»).
Потому что, колеблясь, струна наносит удары по воздуху (газу), а его колебания ударяют по барабанным перепонкам в наших ушах ( а те – по молоточкам, наковаленке… и т.д.). Мозг соображает: ТОН. Звуковая волна какой-то напряжённости, частоты этих самых колебаний.
Это ТОН целой струны какой-то длины (массы отрезка меди). Струна – в роли молоточка для воздуха-наковальни.
Конечно, вряд ли Пифагор и Архит представляли себе физиологию и физику процесса так, как имеем возможность представлять себе мы. Но они заметили: длина струны и ТОН – с о р а з м е р н ы: определённой длине струны соответствует определённый ТОН (частота колебаний).
Прима, первый ТОН (от лат. primas – «первенствующий»):
Если зажимом пережать струну посередине (разделить её надвое) и ударить молоточком (или ущипнуть) ½ струны, уши услышат новый тон – в 2 раза выше (напряжённей) первого, струна будет колебаться в 2 раза чаще. То есть ч а с т о т а к о л е б а н и й ½ струны равна 2 (двум). А полученный тон созвучен первому до невероятно согласного звучания: как будто тот же, только в два раза выше.
Ты уже догадался, что речь идёт об интервале под названием ОКТАВА?
(Интервал – тоже отрезок; отрезок муз. строя).
Того же эффекта можно добиться, если в два раза сильнее натянуть струну, т.е. заранее увеличить её напряжение в два раза.
Итак, ОКТАВА – первый полученный с о в е р ш е н н ы й к о н с о н а н с.
Так и называется: «совершенный консонанс» («совершенная симфония» по-гречески, гармоника).
А длина струны (или волны) и частота её колебаний взаимно зависимы. Зависимы в обратной пропорции: длина – ½, частота – 2.
Экспериментируем (вместе с Пифагором и Архитом) дальше.
Поместим зажим монохорда на отрезке в 2/3 струны (т.е. поделим струну на 3 части и возьмем 2 из трёх частей):
КВИНТА – второй с о в е р ш е н н ы й к о н с о н а н с.
Конечно, тебе известны и другие интервалы.
Хочешь – посчитаем:
- Прима (её тоже причисляют к интервалам).
- Малая секунда. м2
- Большая секунда. Б2
- Малая терция. м3
- Большая терция. Б3
- Чистая кварта. Ч4
- Чистая квинта. Ч5
- Малая секста. м6
- Большая секста. Б6
- Малая септима. м7
- Большая септима. Б7
- Октава.
Двенадцать. Подобно количеству полутонов в октаве. Подобно двенадцати шагам квинт в музыкальном строе.
Правда, есть ещё один странный (мистический!) интервал: увеличенная кварта/уменьшённая квинта – ув.4/ум.5. Один интервал с двумя названиями. Тринадцатый! Ув.4 и ум.5 звучит абсолютно одинаково. Вот каждый раз и думай: «кто есть кто?». Обманчивый какой-то интервал, тревожный. Иногда его называют «волчьей квинтой». Оставим его. У нас-то речь о консонансах и гармонии.
В том музыкальном строе, с которым ты знаком (классический европейский строй), консонансами принято считать ещё и терции и сексты. И кварту.
Но вот что интересно. Классический европейский строй – не единственный в мире. В восточной и современной западной музыке есть музыкальные системы с гораздо бóльшим количеством интервалов (до 53-х!). Однако квинта и октава уже несколько тысячелетий и во всех странах, во всех музыкальных системах остаются главными неизменными интервалами:
С о в е р ш е н н ы м и к о н с о н а н с а м и.
Именно из их градаций/делений образуются все другие интервалы, сколько бы их ни было.
Вот Пифагора интересовала ещё и кварта. Тоже консонанс. Довольно любопытный консонанс. В чём его особенность – мы ещё узнаем.
А пока посмотрим, как Пифагор получил этот интервал.
Струну Пифагор поделил на четыре части и установил зажим между тремя и четвёртой частью: длина струны – ¾. Частота колебаний – 4/3.
Вот теперь внимание! –
Если квинту умножить на кварту – получим… октаву!
По длинам струн (длинам волн): 23 х 34 = 12 длина струны (волны) октавы
По частоте колебаний: 32 х 43 = 2 частота колебаний струны (волны)октавы
А теперь взгляни на клавиатуру:
А вот так? –
Перекрёст!
К этому перекрёсту мы ещё вернёмся.
…
…Ты готов и дальше ломать голову над твоей суперголоволомкой? (Она же – у т е б я в комнате поселилась и живёт!)
Над этой головоломкой ломали голову (в смысле вращали свои мысли) гениальнейшие умы человечества в течение тысячелетий!.. А нам что мешает подключиться?
Подключаемся к волнам мыслей Пифагора…
А что если мы представим себе те волны звука, которые колеблются вместе со струной пифагорова монохорда?
Это – на следующих страничках.
/Рис. автора/
/Рис. автора/
Консонанс – это созвучие, слияние, совпадение звучащих тонов (помнишь?).
В случае с волнами – слияние, совпадение их доминант, кульминаций. Совпадение гребней волн.
/Рис. автора/
Вот интересно: впишется ли в эту стройную систему к в а р т а?
Пифагор кварту тоже относил к консонансам.
А почему бы и нет? Мы же видели несколько страничек назад, что кварты в октаве появились благодаря двум квинтам, двум совершенным консонансам: квинта снизу вверх (от примы к октаве) х квинта сверху вниз (от октавы к приме), в результате их перекрёста. Кроме того, сама октава появляется в результате умножения квинты на кварту: 2/3 х 3/4 = 1/2, 3/2 х 4/3 = 2 (длина волны и частота октавы).
Давай посмотрим:
Не вписывается…
Но ведь не может быть, чтобы не вписалась! Когда-то же это должно случиться!
Мы будем настойчивы, как Пифагор, — раз уж решили следовать волне его мысли:
/Рис. автора/
Наконец-то!
Через 72 маленьких «шажочка»-деления на шкале (12 х 6 = 72) свершился всеобщий консонанс!
Эту ленту из волн можно даже замкнуть в кольцо. Так всё замечательно совпадает.
/Модель автора/
И даже количество кульминаций (гребней волн) соответствует частотам интервалов. Посчитай:
Прима: 6/6 = 1 (частота примы). Вся струна. 1.
Октава: 12/6 = 2 (частота октавы). 1/2 струны.
Квинта: 9/6 = 3/2 (частота квинты). 2/3 струны.
Кварта: 8/6 = 4/3 (частота кварты) 3/4 струны.
Частоты и длины струн ( они же – длины волн) – в обратной пропорции.
Перевёртыш. Перекрёст. Как квинты обращаются в кварты, так и длины волн обращаются в частоты.
Пифагор, конечно, мог сопоставлять вовсе и не волны, а отрезки струн. Например, вот так:
/Рисунки автора/
Хотя, о волнах…
В конце своей жизни Эйнштейн написал автобиографию совершенно особенную. Это была автобиография его м ы ш л е н и я. Из чего рождается научная мысль? – вот о чём была эта автобиография. Как этот процесс в течение жизни он ощущал в себе. «Всё, что мы знаем о реальности, исходит из опыта и завершается им» (Эйнштейн). Мысль начинается с образов реальности. Потом в образах проступает логика. Она становится инструментом сравнений, сопоставлений, которые ведут к закономерностям, а потом – к теории. И – проверка опытом.
«…Это были образы волнующегося моря, символизирующего, а отчасти описывающего недоступные непосредственному зрительному представлению электромагнитные колебания…» (Из книги Б.Г.Кузнецова «Эйнштейн. Жизнь, смерть, бессмертие»)
Волны моря, волны воздуха, волны звука…
Да все древнегреческие памятники архитектуры изрисованы волнами-меандрами!
Ах, как жаль, что Пифагор не оставил нам никаких записей своих мыслей!
И вся его жизнь – легенда, пересказанная учениками учеников-учеников-учеников…
И эта жизнь – всегда у моря, и путешествия – через моря.
/Рисунки из Википедии./
А закон обратной пропорциональности длин волн и частот по сей день управляет волновой физикой. «Струнно-волновая теория» Пифагора… Вот к чему может привести музыка!
Конечно, у волны есть и другие характеристики, помимо длины волны и частоты. Обычно ещё учитывается период колебаний и скорость волны.
/Таблица из Интернет источника: уроки физики/
Но поскольку даже при смене скорости частота волны не меняется, а в нашем случае (на ленте) длина волны и период одинаковы, то мы видим просто явление обратной пропорциональности длины волны и её частоты.
Благодаря наблюдениям Пифагора и его опытам с монохордом был открыт закон гармонических колебаний струны. Посмотри на страничке ниже.
Оказывается, затронутая струна порождает звук, который способен
м о д у л и р о в а т ь (гармонично, или гармонически, изменяться). Звуковая волна, вырвавшись из струны на волю, гармонически модулирует!
Основной тон звучит ясно и громко, а потом превращается в волны повыше и потише. Как эхо, призвуки. И все эти призвуки с о р а з м е р н ы. Их называют ОБЕРТОНАМИ ( ОБЕР-тонами). Иначе эти самые обертоны называют г а р м о н и к а м и. Ну правильно! Они же рождаются из консонансов. А консонансы свидетельствуют о г а р м о н и и.
Гармоники:
/Рис. из Википедии с автор. пометками./
Энциклопедия:
Обертоны (гармоники): от немецкого «обер» — «старший», «высший».
Гармонические призвуки (частичные тоны), имеющиеся в спектре музыкальных звуков. Расположены в ы ш е основного тона, звучат слабее основного тона, сливаясь с ним, на слух почти не распознаются.
Негармонические обертоны свойственны звукам сирен, различным шумам.
Итак, звук, отправившись на волю, на природу, поначалу твердо следует совершенным консонансам – октаве, квинте – затем кварте. А потом… начинает потихоньку расслабляться, шалить. Октавы, квинты, кварты его всё-таки удерживают в рамках какого-то порядка. Но в промежутках всё чаще начинают мелькать словно «разболтанные», колеблющиеся интервалы.
Если эту «прогулку на воле» звуковых волн показать нотами, то она будет выглядеть вот так:
/Рис. из Википедии с пометками автора/
Это — н а т у р а л ь н ы й з в у к о р я д. Латинское natura означает «природа», «естество».
Если верхние звуки попробовать сыграть вместе, боюсь, что консонанса мы уже не услышим. Мы услышим ДИССОНАНС.
Энциклопедия:
Диссонанс – от франц. dissonanse, от лат. dissono – «нестройно звучу».
Неслитное, напряжённое о д н о в р е м е н н о е звучание различных тонов. Противоположность к о н с о н а н с у. К диссонансам относят большие и малые с е к у н д ы и с е п т и м ы, увеличенные и уменьшённые интервалы, а также аккорды, включающие хотя бы один из этих интервалов.
До конца 19 века обязательным считалось разрешение диссонанса в консонанс. С 20 века применяют диссонансы и без их разрешения.
…Да, за диссонансами и до шумов недалеко. До хаоса.
Но ведь г а р м о н и ч е с к и й звукоряд превращается в это! Парадокс!
Хотя, теория хаоса утверждает, что если этот самый хаос предоставить самому себе, в нём опять образуется порядок! Вот такой наш мир, наша жизнь: то консонансы, то диссонансы, то снова консонансы… Такая странная гармония.
Ты понимаешь, чтó мы сейчас делаем?
Конечно, мы играем.
Но уже не только в Узел. В игру внутри игры. Игра – В Пифагора.
В эту игру начали играть спустя 200 лет после Пифагора. Учёные: философы, математики, астрономы-космологи. Все – словно следователи: разгадывают его мысли по обрывочкам древних текстов о его математике и космологии, о его легендарной жизни.
А ещё мы пополняем наше «Досье на тональности», раздел «Родословная»: первопредок ТОН.
И это всё – ну конечно же, о музыке!
***
…Задолго-задолго-задолго до Пифагора тоже была музыка. Какою она была?
Улетела вместе с волнами Времени!
А вот кое-какие знания о ней остались и во времена Пифагора.
Самый-самый древний музыкальный строй в Древней Греции, оказывается, был основан на …пентатонике («пента» — «пять», «тон» — «звук»). Откуда эта пентатоника попала в Древнюю Грецию? Из Древнего Египта, где Пифагор постигал всяческие науки у жрецов больше 20 лет? (А Древний Египет куда древнее Древней Греции! З тыс. лет до н.э.) А в Древний Египет из Персии — через евреев? А в Персию – из Вавилона? (Да Пифагор и сам 12 лет учился у вавилонян.) А Вавилон воздвиг своё царство на земле ещё более древней цивилизации (4 тыс.лет до н.э.) – шумеров. О шумерах остались невероятные легенды (в их числе – о высоком развитии науки и техники), от них же – таблички с решениями уравнений! И пентаграммы, пентагоны… Даже в роли печатей на важных документах. У греков каким-то образом было сообщение и с Китаем, цивилизация которого насчитывает ок. 5 тыс. лет до н. э. А Китай – это вообще страна поклонения пентатонике.
Как бы то ни было, Пифагору предстояло соединить свои открытия с о ч е н ь древними знаниями о мире.
Вот вопрос: интересно, как обозначали музыкальные звуки тысячелетия назад?
Мы привыкли к нотам и буквенным знакам. Но как же прежде?
Может быть, воспользоваться пентагонами-узлами – не такая уж странная идея. Для древних культур это был универсальный знак. А инки узелками могли изложить и обычные сообщения, и математические расчёты, и даже теорию цвета, и знания о космосе…
Возможно, сами свойства названных фигур являлись ключом к познанию всего. Возможно…
Пифагор и его орден (сообщество его единомышленников и учеников) поклонялись пентаграмме. Ты об этом знаешь.
Будем действовать. Экспериментировать.
…Грекам была известна диатоника – звукоряд, образованный квинтами.
ФА – ДО – СОЛЬ – РЕ – ЛЯ – МИ – СИ .
В таком порядке, почему-то, называют звуки диатоники-гептатоники («семитоники»). Не от «до», а от «фа».
Представляешь, какой же это размашистый звукоряд! Нам понадобилась клавиатура, чтобы прошагать по этому ряду звуков. По лестнице квинт.
У Пифагора не было клавиатуры. Первая клавиатура появилась спустя почти тысячу лет после Пифагора.
Клавиатуры не было, а диатоника – была.
Ну и давай попробуем представить её с помощью узелков-пентагонов.
А теперь пропустим нижние узлы. Нам, по законам обертонов струны и природного звукового ряда, можно двигаться только в одну сторону: выше, а значит – вправо. А нижние узлы – левые: движение влево, и… снова вправо.
Но мы всё-таки будем следить за этими нижними узлами, не будем терять их из виду. На всякий случай.
Можем продолжить эксперимент: перевернуть ленту из узлов. Нижние станут верхними.
Потом можно опять перевернуть, и опять перевернуть.
Эти перевёртыши- повороты-вращения, похожие на перекрёсты и обратную пропорциональность, сотворят, наконец-то, привычный звукоряд:
ДО – РЕ – МИ – ФА – СОЛЬ – ЛЯ – СИ.
Диатоническая гамма.
(…перевернуть —)
Что будет, если продолжить ленту ?
Мы сможем это сделать, если совершим одну операцию: перевернём будущее продолжение ленты (такой же её отрезок, как предыдущий: удвоение!) на 180˚, — как это много веков спустя после Пифагора сделал со своей лентой Фердинанд Мёбиус.
Пифагор, безусловно, ничего не мог знать о Мёбиусе. Но он жил в пространстве всё тех же законов природы, что и Мёбиус. И мы живём всё там же. И экспериментируем.
Эту ленту теперь спокойно можно замкнуть в кольцо. И путешествовать по двум поверхностям попеременно, как по одной, — но по обыкновенному кольцу.
Мёбиус наоборот?
/Модели автора/
И ещё одно любопытное наблюдение: каждая нота/звук попеременно оказывается то в «фазе», то в «противофазе». Как волна.
(Лат. phasis – «появление», определённый момент в ходе развития какого-либо процесса.)
Давай вглядимся в процесс, который происходит в кольце с каждым звуком/тоном.
Каждый звук/тон через в о с е м ь шагов обретает своё повторение-совпадение, созвучие – к о н с о н а н с.
А лента-кольцо – сплошной «Мёбиус»: ведь каждый замкнутый узел (пентагон) обладает свойствами «Мёбиуса». Лента-кольцо из узлов замкнула все узлы разом.
Замкнутые в кольцо узлы-звуки произвели на свет о к т а в у: греч. «окто» — «восемь», лат. octava – «восьмая». Совершенный консонанс.
Один совершенный консонанс – квинта — произвёл на свет другой совершенный консонанс – октаву.
Если убрать пропущенные нижние левые узлы, то размашистая лента квинт сожмётся в д в о е. Как окружности в геометрической прогрессии!………………………………………………………………….
(О, прости, вот в этом самом месте мою мысль просто-таки примагнитило к одной увлекательной идее. Через несколько страниц/листочков вернёмся к Пифагору.)
ЛИСТОЧКИ «МЫСЛЕЙ ВБОК»
(о геометрической прогрессии)
(Следующие 9 страниц можно пропустить, а можно и полюбопытствовать…)
/Рис. автора/
/Рис. автора/
/Рис. автора/
/Рис. автора/
/Рис. автора/
/Фрагменты статьи из Википедии/
Итак, Пифагору предстояло провести операцию сжатия размашистых квинт.
Этот п р о ц е с с ты буквально сможешь ощутить своими руками, если не поленишься сделать простенькую модель из узлов.
А что? Пифагор ведь тоже догадался незримое (звук) исследовать с помощью п р е д м е т а – струны.
Растяни узлы в волну, а потом начни складывать «гармошкой».
…Ты ощущаешь, как узлы/квинты закручиваются в винт?
Теперь не очень плотно складывай, — так, чтобы видеть названия нот.
…Винтовая лестница!
Посмотри сбоку.
А теперь изобразим ступеньки этой лестницы под прямым углом:
Нижние квинты спрятались совсем. Словно исчезли, как тени в полдень.
И мы теперь видим привычные нам ступени гаммы.
Как их обозначали древние греки? Как они называли сами звуки? – Мы пожимаем плечами.
Если верить историкам музыки, первые попытки записывать музыкальные звуки знаками, появились не раньше 11 века. И выглядели эти знаки как просто точки или квадратики на двух линейках. Названия этих звуков/знаков тоже появились в Средние века, через полтора с лишним тысячелетия после Пифагора.
А вот ступени могли обозначаться числами. А числа записывались буквами греческого алфавита. А древнегреческий алфавит уж наверняка отличался от нынешнего.
Вот поэтому удобнее иметь дело с геометрическими образами.
Геометрия сама всё показывает.
А пересказывать то, что показывает геометрия, мы будем на привычном нам языке. Так и поступают исследователи музыки. Они переводят древние знания на привычные нам языки с их знаками: буквы латинского (или
русского) алфавита (вот! греческие названия нот даже не употребляются), арабские (индийские) и латинские цифры для обозначения чисел.
Для пифагорова музыкального строя имеют значение именно интервалы.
Сами характеристики отдельных звуков выражены как интервалы: то есть каждый звук определяется отношением к другому звуку (вот где корни относительности!). Первый взятый звук становится точкой отсчёта (точкой опоры). А все остальные звуки находятся по законам гармонии, консонансов:
Первый консонанс – ПРИМА ( двойной первый звук, унисон, сам себе консонанс: 1/1).
Второй консонанс – ОКТАВА (второй из двойного звука ПРИМЫ растянулся в диапазон-ОКТАВУ: 1-2, второй звук по отношению к первому, 2/1).
Третий консонанс – КВИНТА (третий звук по отношению ко второму : 3/2 ).
Четвёртый консонанс – КВАРТА (четвёртый звук по отношению к третьему : 4/3 и в то же время – это перевёрнутая квинта, отношение октавы к квинте; 2:3/2, или 2х2/3=4/3).
Таким образом, каждому звуку присваивается своя дробь, — которая, собственно и является знаком о т н о ш е н и я.
То есть, в каждом звуке уже спрятан интервал ( интервал/расстояние/отрезок струны/волны или отрезок «пробега» волны по частотам, как в нашей ленте частот).
И, получается, только в Средние века этим дробям/отношениям дали буквенные (или слоговые) названия, которыми мы и пользуемся:
1/1, прима – ДО1.
2/1, октава – ДО2.
3/2, квинта – СОЛЬ.
4/3, кварта – ФА
Если интересно, найди в Интернете статью «Как появились названия нот?».
А я приведу здесь небольшие отрывки из этой статьи /сайт: muz-teoretik.ru/
Пифагор оперировал только числами.
Он поклонялся Числу, словно божеству.
Все вещи мира, все явления можно выразить Числом! – вот главная идея его вдохновенного мышления.
Все названия звуков, которые он находил, происходят от чисел. И названия интервалов – от чисел.
Мы, конечно, будем пользоваться именами звуков для лучшего понимания, но всегда будем иметь в виду, что за этими именами – числа.
Вот и наша лестница квинт пронумерована числами-ступенями.
Головокружительно вот что:
Получается, что каждый звук этой лестницы – этакая микроквинта.
Хотя, в общем-то, ничего особенно удивительного в этом и нет, если вспомнить, что у квинты – функция (роль) д о м и н а н т ы – высшего напряжения, высшего проявления какого-то качества, характера. В нашем случае – максимум проявления характера каждого звука, его особенности.
Дух захватывает только когда осознаёшь, что на пятой ступени лестницы мощность отдельного звука-микроквинты (соль) словно пятикратно возрастает: квинта, да ещё и в положении КВИНТЫ в октаве! Квинта обретает новый масштаб! Она п о д о б н а себе, но уже в ином масштабе.
Этот процесс можно увидеть страничкой ниже.
А что же остальные звуки?
Сохранились ли в них хотя бы намёки на их «первородство» — на квинту?
Давай посмотрим на одну таблицу. Она показывает следующий этап процесса сотворения музыкального строя Пифагором: вычисленные им остальные звуки октавы.
Для удобства понимания на ней указаны имена звуков, но за каждым из них – Число! (по-«пифагоровски»). /ниже – таблица из книги: Волошинов М.В. «Математика и искусство». М. Просвещение, 1992г.//
Да, как-то хитро запрятались квинты внутрь других звуков. И не распознаешь их с первого взгляда.
Кстати, ты заметил, что все числа – это частоты: числитель дробей больше знаменателя, «большее на меньшее», большее число в отношении к меньшему. У длин волн – наоборот: меньшее число в отношении к большему. Надеюсь, ты помнишь про этот перевёртыш/перекрёст.
Да и сам первый звук (прима) уже словно намекает на то, что предстоит увлекательная игра в перевёртыши: если частоту звука умножить на длину его волны, то и получится е д и н и ц а, начало отсчёта.
А если частоту квинты умножить на частоту её перевёртыша – частоту кварты, — получится октава (по частоте). Или перемножить длины волн квинты и её перевёртыша кварты, — будет октава по длине волны. Этакий расширенный, удвоенный перевёртыш.
Да и сама октава – удвоенная единица-прима: 2. Или поделённая пополам: ½.
( Опять – геометрическая прогрессия?!)
Прима – нижняя граница звукоряда. Октава – верхняя граница.
В середине – квинта и её перевёртыш кварта.
Да, по-видимому, Пифагор понял, что отношения между этими звуками и интервалы, которые образуются из их отношений, и должны стать ключом к поиску характеристик других звуков – их частот и длин волн.
Давай-ка ещё разочек обратимся к ленте частот.
О, этот долгий путь ко всеобщему консонансу и гармонии!
Путь получился долгим из-за того, что квинте пришлось вращаться-обращаться в кварту, и это вращение-обращение должно было прийти к консонансу в конце концов.
Отношения частот прямой квинты и её обращения кварты произвело на свет новое отношение и новый звук: 9/8.
9/8. Девять кульминаций квинты к восьми кульминациям кварты.
В таблице – это звук РЕ. II ступень.
То же самое отношение получится, если перевернуть кварту и умножить этот перевёртыш на квинту. (Перевёртыш перевёртыша – просто голова крýгом!)
Если результат этой операции умножить на результат такой же операции (результат в квадрате), то есть 9/8 х 9/8, получим следующий звук.
9/8 х 9/8 = 81/64
Получилась частота МИ. III ступень.
Следующая ступень, IV, нам известна: кварта, 4/3.
Умножим 81/64 (ми) на 4/3 (фа): 81/64 х 4/3 = 27/16.
Это частота ЛЯ, VI ступень.
Её же можно получить, «воспользовавшись услугами» известной нам Vступени, квинты: умножить квинту 3/2 на тон 9/8. 3/2 х 9/8 = 27/16.
VII-ю ступень, СИ, мы получим, умножив частоту ЛЯ опять же на тон 9/8:
27/16 х 9/8 = 243/128
Между прочим, если мы и кварту 4/3 умножим на тон 9/8, то получим квинту: 4/3 х 9/8 = 3/2
…И все эти числа – реально звучат!
106
… А ты заметил, что ТОН/звук у нас теперь фигурирует и в качестве
р а с с т о я н и я между звуками?
Удивительно: ТОН – и сам звук, и в то же время – расстояние между звуками в октаве!
Может, это – из-за в о л н ы?
Ведь звуковая волна «пробегает» р а с с т о я н и е.
Вспомни ленту частот. Волне примы пришлось «пробежать» шесть своих расстояний, пока не свершился Великий Консонанс: созвучие примы, октавы, квинты и кварты.
А ведь прима – ТОН, с которого всё начинается, чтобы прийти к октаве. А шесть «пробежек» приме пришлось совершить из-за отношений квинты и кварты (перевёртыша квинты).
Вот так всё и сошлось: в октаве должно быть шесть тонов, а каждый тон выражает отношение между квинтой и квартой: девять кульминаций квинты к восьми кульминациям кварты – 9/8.
Да может быть, и сама октава (от греч. «окто» — «восемь») получила такое название из-за этих самых восьми кульминаций кварт!
Кварта (то есть квинта наоборот) «виновата»!
И даже отношение октавы (восемь её ступеней) к шести тонам указывает на эту «виновницу»! 8/6 = 4/3
…Вернёмся, однако, к сотворению октавы. Ещё не всё завершено в ней.
Тонов должно быть ш е с т ь, а у нас набирается пока что целых тонов всего пять:
Заметим попутно: тон между ФА и СОЛЬ назван р а з д е л и т е л ь н ы м.
Почему? А посмотри:
Вспомнил эту картинку? Квинта снизу вверх в октаве и её перевёртыш сверху вниз и образуют этот самый разделительный тон. И разделяют октаву на две кварты: ДО1-ФА и СОЛЬ-ДО2. Они одинаковы. И в каждой – по два целых тона и «остаток». Тоже одинаковый.
Существует несколько способов его вычислить.
Давай попробуем это сделать, исходя из той простой мысли, что «остаток» предполагает деление.
Итак, в кварте ДО1-ФА частоту ФА разделим на частоту соседнего МИ:
4/3:81/64 = 4/3х64/81 = 256/243
В кварте СОЛЬ-ДО2 частоту ДО2 разделим на частоту соседнего СИ:
2:243/128 = 2х128/243 = 256/243
Таблица, которую ты увидишь сейчас, — совершенно замечательная таблица!
Что в ней стóит заметить?
С одной стороны, она похожа на таблицу предыдущую.
А вот с другой стороны… Взгляд с другой стороны – это тот же перевёртыш. Мысленный перевёртыш.
И в самой таблице мы увидим перевёртыш: сами звуки показаны как частоты, а расстояния между звуками – как длины.
/Основная таблица – из Интернет источника в свободном доступе/
Обрати внимание на РЕ (D). Под самим звуком указана его частота. А расстояние от РЕ (D) до примы ДО (С) – как д л и н а в о л н ы РЕ. Выходит, наша гипотеза о происхождении расстояний между звуками из-за того, что волны обладают длиной (или периодом), имеет всё-таки основание.
И главной мерой расстояний между звуками стал ТОН.
Давай-ка ещё разочек заберёмся внутрь этого самого ТОНА, вглядимся в него:
То что мы называли «кульминацией» на музыкальном языке, на языке физики «импульс».
Энциклопедия:
Импульс: от лат. impulsus — «удар», «толчок»; всплеск, усилие, побуждение.
Звуковой импульс – внезапно и быстро исчезающее повышение давления.
Изменение напряжения.
Усилие, напряжение – ведь это же главные свойства д о м и н а н т ы! И главные характеристики к у л ь м и н а ц и и.
А в физике — и м п у л ь с.
На языке физики мы бы сказали, что волна п р и м ы имеет ш е с т ь импульсов (если посмотрим на нашу полосу частот); волна о к т а в ы имеет д в е н а д ц а т ь импульсов; волна к в и н т ы имеет д е в я т ь импульсов; волна к в а р т ы имеет в о с е м ь импульсов. И все они словно борются друг с другом, то соединяясь, то противостоя, усиливая и погашая усилия друг друга, — пока не придут ко всеобщему согласию через какой-то диапазон/расстояние. И тогда все их усилия соединяются в согласии.
Физики бы сказали, что в этом моменте наступает резонанс.
Латинское слово resono – «откликаюсь»; resonans – «отзвук» (sono – звук, re – поворот).
Вот! В диапазоне октавы после согласия-резонанса наступает поворот-отражение. Октава – словно зеркало, в котором квинта отражается в кварту! И все остальные звуки отражаются в обратном порядке. Повороты-перевёртыши. И… с и м м е т р и я: левое – отражение правого, правое – левого. И так – опять до примы, пока не замкнётся кольцо. И всё повторится снова.
Все интервалы в октаве – симметрично отражаются:
Октава – отражение примы; септима – отражение секунды; секста – отражение терции.
Кварта – отражение квинты. Но… со смещением от центра симметрии!
Если бы квинта отразилась строго в центре симметрии, получились бы два
д и с с о н и р у ю щ и х, два самых сверхнапряжённых интервала, тех самых, которые называют «волчьими квинтами» (увеличенная кварта, или уменьшённая квинта). И тогда всю музыку пришлось бы промерять этими «воющими» интервалами! Всю – начиная с диатоники. Представляешь, вся музыка превратилась бы в вой! И вместо гармонии – хаос!
Квинта должна была сохранить свою чистоту – остаться чистой квинтой.
И отразиться чистой квартой.
Это возможно только в том случае, если и расстояния между звуками будут подобны квинте.
И в самом деле, взгляни на знакомую таблицу, — и ты увидишь, что звуки с их высчитанными частотами словно сами собой распределились по расстояниям в соответствии с квинтой: два тона – три тона. 2/3. По длине волны квинты.
А оставшийся ш е с т о й тон стал границей, разделом, — сам поделившись надвое.
Сами звуки расположились симметрично, по квартам. А расстояния между ними – асимметрично, по квинтам.
Симметрия и асимметрия – в одном.
Симметрия и асимметрия в одной октаве.
Симметрия и асимметрия в отрезке (октава – интервал, интервал – отрезок).
Быть может, ты вспомнишь, где нам встречалось это явление: сочетание симметрии и асимметрии вместе?
… «ДЕЛЕНИЕ ОТРЕЗКА В КРАЙНЕМ И СРЕДНЕМ ОТНОШЕНИИ»…
…Ну, конечно же… Золотое сечение!
Но вместе всё это сотворяет особую симметрию – САМОПОДОБИЕ.
/Рис. автора/
Геометрические мысли о консонансах
/Модель автора/
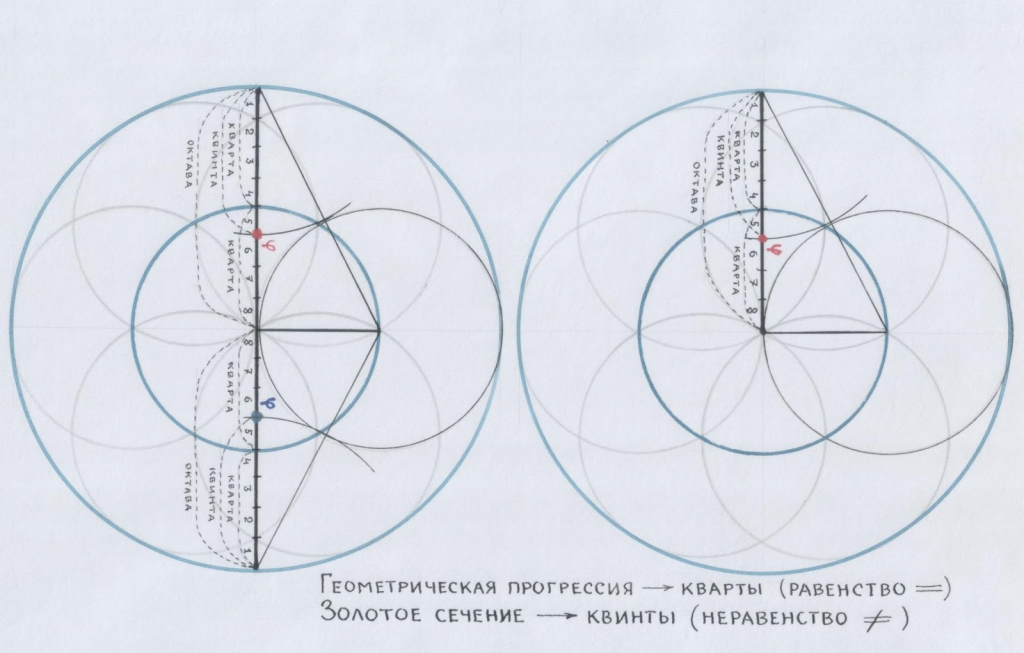
/Рис. автора/
/Рис. автора/
…Ох, это Золотое сечение! Куда ни взглянешь – машет ручкой: привет-привет! А уж на клавишах так прямо само в глаза бросается: вот оно я! Вот же!
Как же Пифагор обходился без клавиш?
Ну не было их тогда. Вместо клавиш – геометрия! Отрезки, пропорции, числа-дроби.
Вот и та, последняя, таблица, с интервалами-отрезками между звуками октавы… Мы в ней далеко не всё интересное разглядели и обмыслили.
Слово там одно необычное не даёт покоя.
Ты видишь его, это слово?
/Табл. из Интернет источника в свободном доступе/
…ЛИММА.
Зачем здесь такое странное слово?
Странное. Но какое красивое!
Греческое.
А означает – «остаток». Всего лишь! Так просто…
Однако греки и любили-то именно сочетание простоты и красоты.
Ну сравни сам, вслушайся: «полутон» и … Лимма, Леймма… Это же музыка!
Даже в простом слове – музыка.
Энциклопедия:
Ли́мма (устар. ле́ймма) (греч. λεῖμμα — остаток, лат. limma, реже leimma) — музыкальный интервал, соответствующий диатоническому полутону (малой секунде) пифагорова строя. Согласно античному определению, восходящему к пифагорейской школе, лимма равна разности чистой кварты и двух целых тонов (отсюда название как «остатка» кварты после отделения от неё двух целых тонов) и, таким образом, имеет отношение частот верхнего и нижнего звука, равное
4/3 : (9/8)² = 256/243
Не думаю, что оставшиеся странички этой тетради ты бы (вдруг!) прочитал «взахлёб». Они сухи, как осенние листья, как древние папирусы. Царапины Истории. В них не ощущается той жгучей эмоции, которая воспламеняет любопытство и азарт следователя, напавшего на след тайны. А ведь изначально было именно так! У Платона, у Боэция, и ещё у многих. Они – и тайна Пифагора. И благодаря им мы тоже теперь причастны этой тайне. И тоже – будто следователи. Увлечены.
Пламя притушено, эмоции высушены «учёным стилем» и временем. Просто исторические документы. И даже – всего лишь какие-то лоскутки текстов в этих документах.
Хочешь – взгляни. А вдруг у тебя получится угадать за этим – п о и с к.
/ «Афинская школа» Рафаэля. Фрагмент. Пифагор./
/Википедия/
